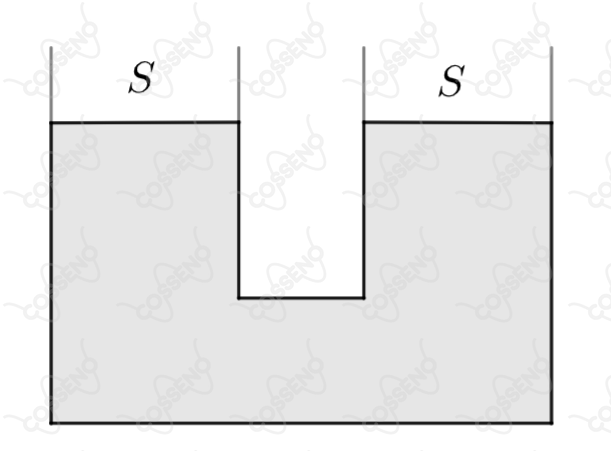
Os dois vasos comunicantes a seguir são abertos, têm seções retas iguais a e contêm um líquido de massa específica . Introduz-se no vaso esquerdo um cilindro maciço e homogêneo de massa , seção e menos denso que o líquido. O cilindro é introduzido e abandonado de modo que no equilíbrio seu eixo permaneça vertical. Podemos afirmar que no equilíbrio o nível de ambos os vasos sobe:
CossenoGPT
Teste
gratuitamente agora
mesmo! 

Primeiramente, observe que no equilíbrio as duas superfícies do líquido devem continuar na mesma altura, portanto ambas sobem da mesma quantidade.
Seja $L$ o comprimento submerso do cilindro, como o empuxo é igual ao seu peso, temos que $$\rho S' L g = M g$$
logo $$L = \frac{M}{\rho S'}$$ O volume de água deslocado é $V = LS' = \frac{M}{\rho}$. Ademais, o volume deslocado é dividido nas duas colunas do tubo. Assim, sendo $h$ o aumento da altura da superfície do líquido, $V = 2Sh$, portanto $h = \frac{V}{2S} = \frac{M}{2\rho S}$ $=>$ Opção E

