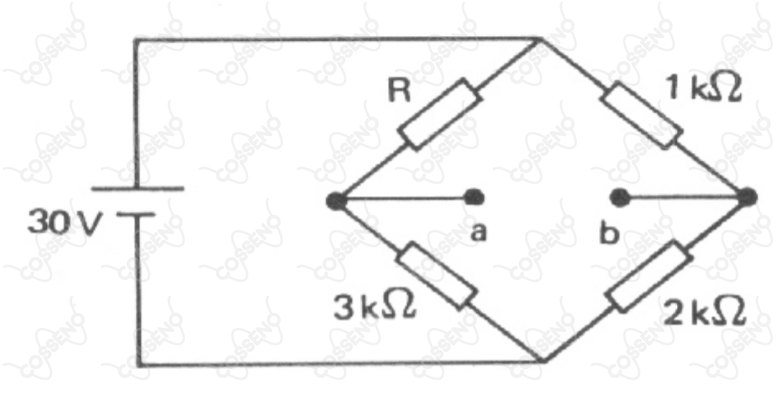
A ponte de resistores a seguir apresenta na temperatura ambiente uma tensão entre os seus terminais e . Considerando que a resistência está imersa em um meio que se aquece a uma taxa de graus centígrados por minuto, determine o tempo que leva para que a tensão entre os terminais e da ponte se anule. Considere para a variação da resistência com a temperatura um coeficiente de resistividade de .
CossenoGPT
Teste
gratuitamente agora
mesmo! 

Podemos começar redesenhando a situação, e denotando alguns elementos como abaixo:
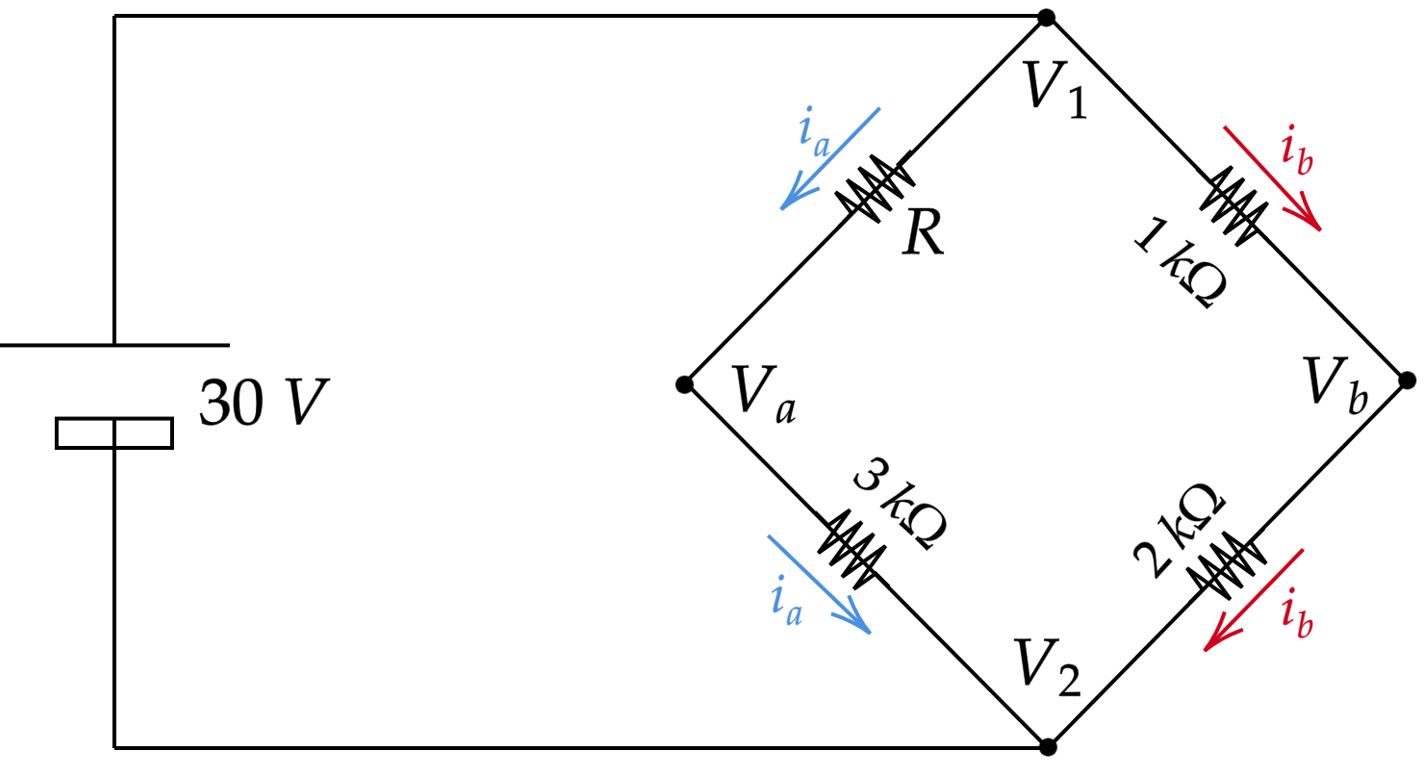 Pela $\text{Primeira Lei de Ohm}$: \begin{matrix} V_1 - V_2 = (1+2).i_b &\therefore& i_b = 10 \ mA
\end{matrix}Continuando, \begin{matrix} \begin{cases} V_a - V_2 = 3.i_a \\ V_1 - V_b = 1.i_b
\end{cases}&\Rightarrow& (V_a - V_b) + (V_1 - V_2) = 3.i_a + i_b &\therefore& i_a = 7,5 \ mA
\end{matrix}Assim, \begin{matrix} \begin{cases} V_1 - V_a = R.i_a \\ V_b - V_2 = 2.i_b
\end{cases}&\Rightarrow& (V_1 - V_2) - (V_a - V_b) = R.i_a + 2.i_b &\therefore& R = 1 \ k \Omega
\end{matrix}Para que a tensão dos terminais se anule, deve-se ter a relação da $\text{Ponte de Wheatstone}$, logo: \begin{matrix} R^{*}.2 = 1.3 &\therefore& R^{*} = 1,5 \ k \Omega
\end{matrix}
Com isso, a resistência deve variar $\Delta R = 0,5 \ k \Omega$, adiante, sabida a $\text{Segunda Lei de Ohm}$, temos a expressão aproximadamente válida:\begin{matrix} \Delta R = R.\alpha.\Delta \theta &\Rightarrow& 0,5.10^3 =1.10^3 \ . \ 4,1.10^{-3} \ . \ \Delta \theta &\therefore& \Delta \theta = 122 K
\end{matrix}Portanto, como o meio aquece $10$ graus centígrados por minuto, concluí-se:\begin{matrix} t = \frac{1 \ min}{10 \ K}. 122 \ K &\therefore& \fbox{$t \cong 12 \ \text{minutos} \ e \ 12 \ \text{segundos}$}
\end{matrix}\begin{matrix}Letra \ (B)
\end{matrix}
Pela $\text{Primeira Lei de Ohm}$: \begin{matrix} V_1 - V_2 = (1+2).i_b &\therefore& i_b = 10 \ mA
\end{matrix}Continuando, \begin{matrix} \begin{cases} V_a - V_2 = 3.i_a \\ V_1 - V_b = 1.i_b
\end{cases}&\Rightarrow& (V_a - V_b) + (V_1 - V_2) = 3.i_a + i_b &\therefore& i_a = 7,5 \ mA
\end{matrix}Assim, \begin{matrix} \begin{cases} V_1 - V_a = R.i_a \\ V_b - V_2 = 2.i_b
\end{cases}&\Rightarrow& (V_1 - V_2) - (V_a - V_b) = R.i_a + 2.i_b &\therefore& R = 1 \ k \Omega
\end{matrix}Para que a tensão dos terminais se anule, deve-se ter a relação da $\text{Ponte de Wheatstone}$, logo: \begin{matrix} R^{*}.2 = 1.3 &\therefore& R^{*} = 1,5 \ k \Omega
\end{matrix}
Com isso, a resistência deve variar $\Delta R = 0,5 \ k \Omega$, adiante, sabida a $\text{Segunda Lei de Ohm}$, temos a expressão aproximadamente válida:\begin{matrix} \Delta R = R.\alpha.\Delta \theta &\Rightarrow& 0,5.10^3 =1.10^3 \ . \ 4,1.10^{-3} \ . \ \Delta \theta &\therefore& \Delta \theta = 122 K
\end{matrix}Portanto, como o meio aquece $10$ graus centígrados por minuto, concluí-se:\begin{matrix} t = \frac{1 \ min}{10 \ K}. 122 \ K &\therefore& \fbox{$t \cong 12 \ \text{minutos} \ e \ 12 \ \text{segundos}$}
\end{matrix}\begin{matrix}Letra \ (B)
\end{matrix}

Ampliar Imagem

