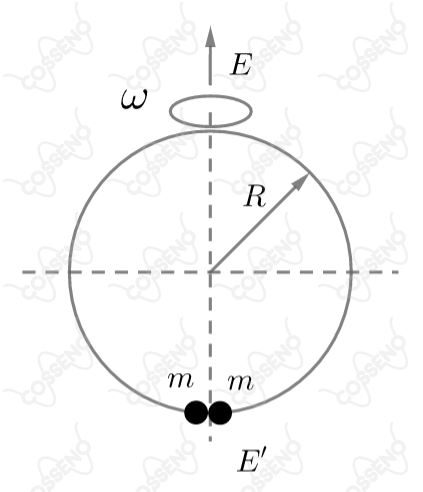
Um aro metálico circular e duas esferas são acoplados conforme ilustra abaixo. As esferas dispõem de um furo diametral que lhes permite circular pelo aro. O aro começa a girar, a partir do repouso, em torno do diâmetro vertical , que passa entre as esferas, até atingir uma velocidade angular constante . Sendo o raio do aro, a massa de cada esfera e desprezando-se os atritos, pode afirmar que:
CossenoGPT
Teste
gratuitamente agora
mesmo! 

Analisando a situação, pode-se perceber que atuam apenas duas forças em cada esfera, no caso, a força peso e a reação de contato da esfera com o aro. Nesse viés, conforme a frequência angular aumenta, o ângulo $\theta$ de abertura aumenta até certo ponto (veremos isso abaixo), as esferas ascendem até uma posição arbitrária, a qual podemos esboçar como:
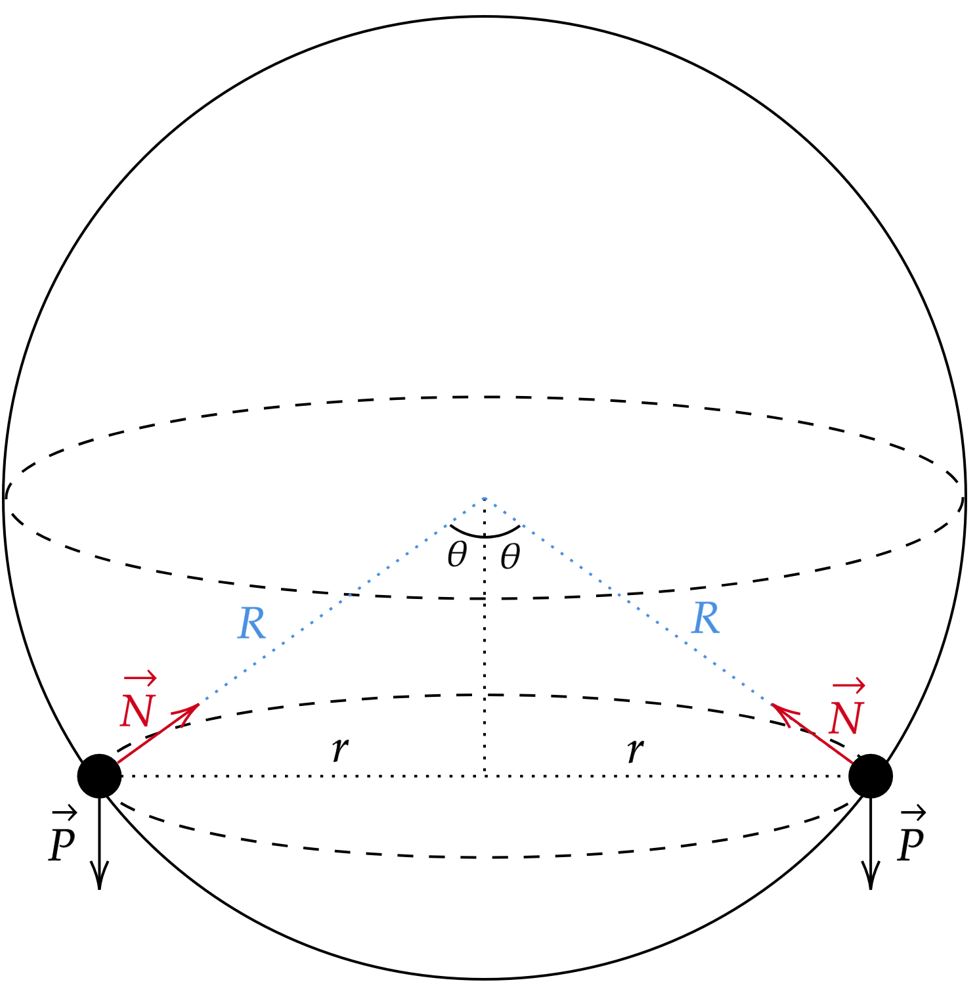 Atente que, é racional pensar que as esferas estejam abaixo do diâmetro horizontal, do contrário, seria necessário uma outra força - diferente do peso e da normal - para manter o equilíbrio vertical. Com isso, decompondo a reação de contato $\vec{N}$, têm-se a componente horizontal responsável pelo movimento circular, além da componente vertical, esta responsável pelo equilíbrio vertical das esferas. Analisando uma das esferas, constata-se:\begin{matrix}\begin{cases}
N \cos{\theta} = P \\
N\sin{\theta} =R_c
\end{cases}&\Rightarrow& m \cdot \omega^2 \cdot r = N \sin{\theta} &\Rightarrow& m \cdot \omega^2 \cdot r = P \tan{\theta} &\therefore& \tan{\theta} = \dfrac{\omega^2 \cdot r}{g}
\end{matrix}\begin{matrix}Letra \ (B)
\end{matrix}$\color{orangered}{Obs:}$ Paras as esferas estarem sobre o diâmetro, $\theta = 90^{\circ}$, porém, $\tan{90^{\circ}} = \nexists$, o que inviabiliza o equilíbrio nessa posição.
Atente que, é racional pensar que as esferas estejam abaixo do diâmetro horizontal, do contrário, seria necessário uma outra força - diferente do peso e da normal - para manter o equilíbrio vertical. Com isso, decompondo a reação de contato $\vec{N}$, têm-se a componente horizontal responsável pelo movimento circular, além da componente vertical, esta responsável pelo equilíbrio vertical das esferas. Analisando uma das esferas, constata-se:\begin{matrix}\begin{cases}
N \cos{\theta} = P \\
N\sin{\theta} =R_c
\end{cases}&\Rightarrow& m \cdot \omega^2 \cdot r = N \sin{\theta} &\Rightarrow& m \cdot \omega^2 \cdot r = P \tan{\theta} &\therefore& \tan{\theta} = \dfrac{\omega^2 \cdot r}{g}
\end{matrix}\begin{matrix}Letra \ (B)
\end{matrix}$\color{orangered}{Obs:}$ Paras as esferas estarem sobre o diâmetro, $\theta = 90^{\circ}$, porém, $\tan{90^{\circ}} = \nexists$, o que inviabiliza o equilíbrio nessa posição.

Ampliar Imagem

