Num triângulo , retângulo em , temos . As bissetrizes destes ângulos se encontram num ponto . Se o segmento de reta mede , então a hipotenusa mede:
CossenoGPT
Teste
gratuitamente agora
mesmo! 

$• \ \text{Resolução I:}$ O ponto de encontro das bissetrizes é chamado de incentro, este que também é o centro da circunferência inscrita no triângulo. Nesse contexto, seja $R$ o raio da circunferência inscrita, esboçando-se a situação, denotemos por $E$ o ponto de tangência entre o lado $\overline{AB}$ e a circunferência. Dessa forma, temos três triângulos retângulos, os quais usaremos para encontrar o lado $\overline{BC}$, assim, comecemos encontrando $\overline{AB}$ : \begin{matrix} B\hat{E}D = 30º & \Rightarrow & \cos{30º} = \dfrac{\overline{EB}}{\overline{BD}} = \dfrac{\overline{EB}}{1} &\therefore&
{\overline{EB} = \dfrac{\sqrt{3}}{2}}
\end{matrix}Repara agora que, \begin{matrix} \overline{ED} = \overline{AE} = R \\ \color{gray}{\text{O triângulo retângulo $ADE$ é isósceles}}
\end{matrix}Assim, \begin{matrix} B\hat{E}D = 30º & \Rightarrow & \sin{30º} = \dfrac{\overline{ED}}{\overline{BD}} = \dfrac{R}{1} &\therefore&
{R = \dfrac{1}{2}}
\end{matrix}Continuando, \begin{matrix} \overline{AB} = \overline{AE} + \overline{EB} &\Rightarrow& \overline{AB} = \dfrac{1}{2} + \dfrac{ \sqrt{3}}{2}
\end{matrix}Agora, no triângulo $ABC$, temos: \begin{matrix} \sin{30º} = \dfrac{\overline{AB}}{\overline{BC}} &\therefore& \fbox{$ \overline{BC} = (1 + \sqrt{3}) \ \pu{cm} $}
\end{matrix}\begin{matrix}Letra \ (B)
\end{matrix}
$• \ \text{Resolução II:}$ Esboçando a situação, primeiro vamos encontrar alguns ângulos, denotemos por $E$ o ponto que liga a bissetriz de $A$ ao lado $\overline{BC}$, assim: \begin{matrix} B\hat{D}E = B\hat{A}D + A\hat{B}D &\Rightarrow& B\hat{D}E = 45º + 30º &\therefore& B{\hat{D}E = 75 º}
\end{matrix}Perceba que, $ADE$ é isósceles, isto é, o lado $ \overline{BE} = 1$. Pela lei dos cossenos no triângulo $ADE$, podemos encontrar $\overline{DE}$: \begin{matrix} \overline{DE}^2 = 1^2 + 1^2 - 2\cdot 1\cdot 1\cdot \cos{30º} &\Rightarrow& { \overline{DE}^2 = 2 - \sqrt{3} }
\end{matrix}Note que, com o ângulo $B\hat{D}E$, podemos encontrar o ângulo $C\hat{E}D$ e, por conseguinte, o ângulo $C\hat{D}E$: \begin{matrix} C\hat{E}D = 180º - B\hat{D}E \\ {C\hat{E}D = 105º} \\ C\hat{D}E = 180º - C\hat{E}D - D\hat{C}E = 180º - 105º - 15º \\ {C\hat{D}E = 60º}
\end{matrix}Aplicando a lei dos senos no triângulo $CDE$: \begin{matrix} { \dfrac{\overline{EC}}{ \sin{60º}} = \dfrac{\overline{DE}}{ \sin{15º}}}&,& {{\cos{30º} = 1 - 2.\sin^2{15º}}} &\Rightarrow&
{ \overline{EC} = \sqrt{3} }
\end{matrix}Por fim, o lado $\overline{BC}$: \begin{matrix} \overline{BC} = \overline{BE} + \overline{EC} &\therefore& \fbox{$ \overline{BC} = (1 + \sqrt{3}) \ \pu{cm} $}
\end{matrix}
$• \ \text{Resolução III:}$ Num caminho análogo ao do começo da resolução II (encontrando ângulos), podemos aplicar a lei dos senos no triângulo $BCD$, vejamos: \begin{matrix} { \dfrac{\overline{BC}}{ \sin{135º}} = \dfrac{\overline{BD}}{ \sin{15º}}} & \Rightarrow& \fbox{$ \overline{BC} = (1 + \sqrt{3}) \ \pu{cm} $}
\end{matrix}
Solução Alternativa - Centro de massa:
O Incentro - Ponto de encontro das bissetrizes - É o ponto de equilíbrio do triangulo com "massas" em seus vértices, correspondentes às medidas dos lados opostos. Assim, sendo A, B e C os vértices do triângulo, e $a$, $b$ e $c$ as medidas dos lados opostos aos respectivos vértices, colocando uma massa de "peso" $a$ em A, uma massa de "peso" $b$ em B e uma massa de "peso" $c$ em C, o triangulo deve ficar equilibrado no incentro;
Desta forma, podemos seguir para a resolução:
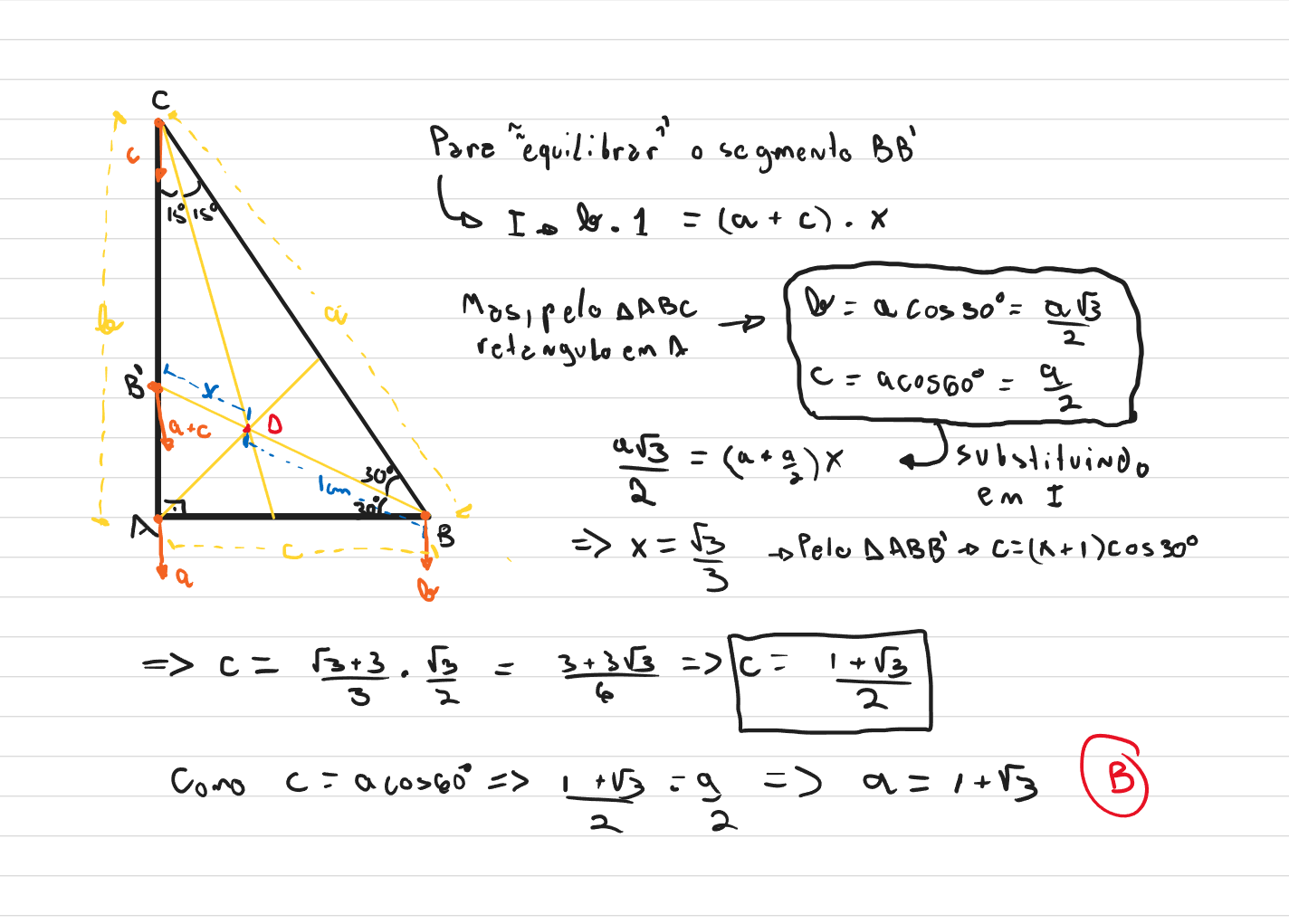

Ampliar Imagem

21:43 23/04/2024
Não costumo enviar resoluções, mas achei essa forma muito legal e decidi compartilhar, se houver algum erro me avisem!


