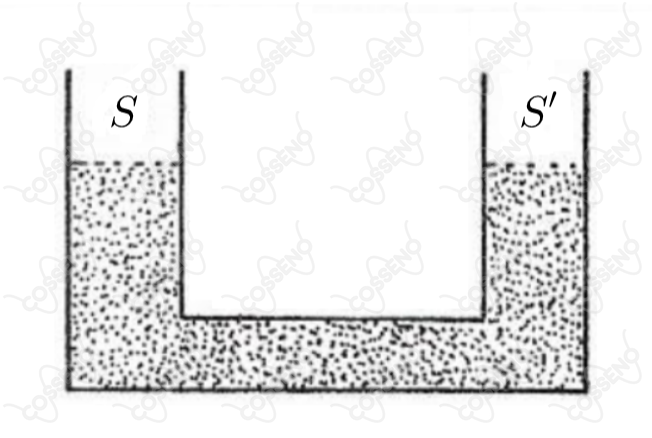
O sistema de vasos comunicantes da figura cujas secções retas são e , está preenchido com mercúrio de massa específica . Coloca-se no ramo esquerdo um cilindro de ferro de massa específica , volume e secção . O cilindro é introduzido de modo que seu eixo permaneça vertical. Desprezando o empuxo do ar, podemos afirmar que no equilíbrio:
CossenoGPT
Teste
gratuitamente agora
mesmo! 

Analisando a situação, pode-se inferir que $S^{''}$ é menor que $S$, logo, pelo $\text{Teorema de Stevin}$ sabemos que não haverá desnível da água, mas sim que o nível irá subir. Nesse viés, é possível se esboçar a situação como:
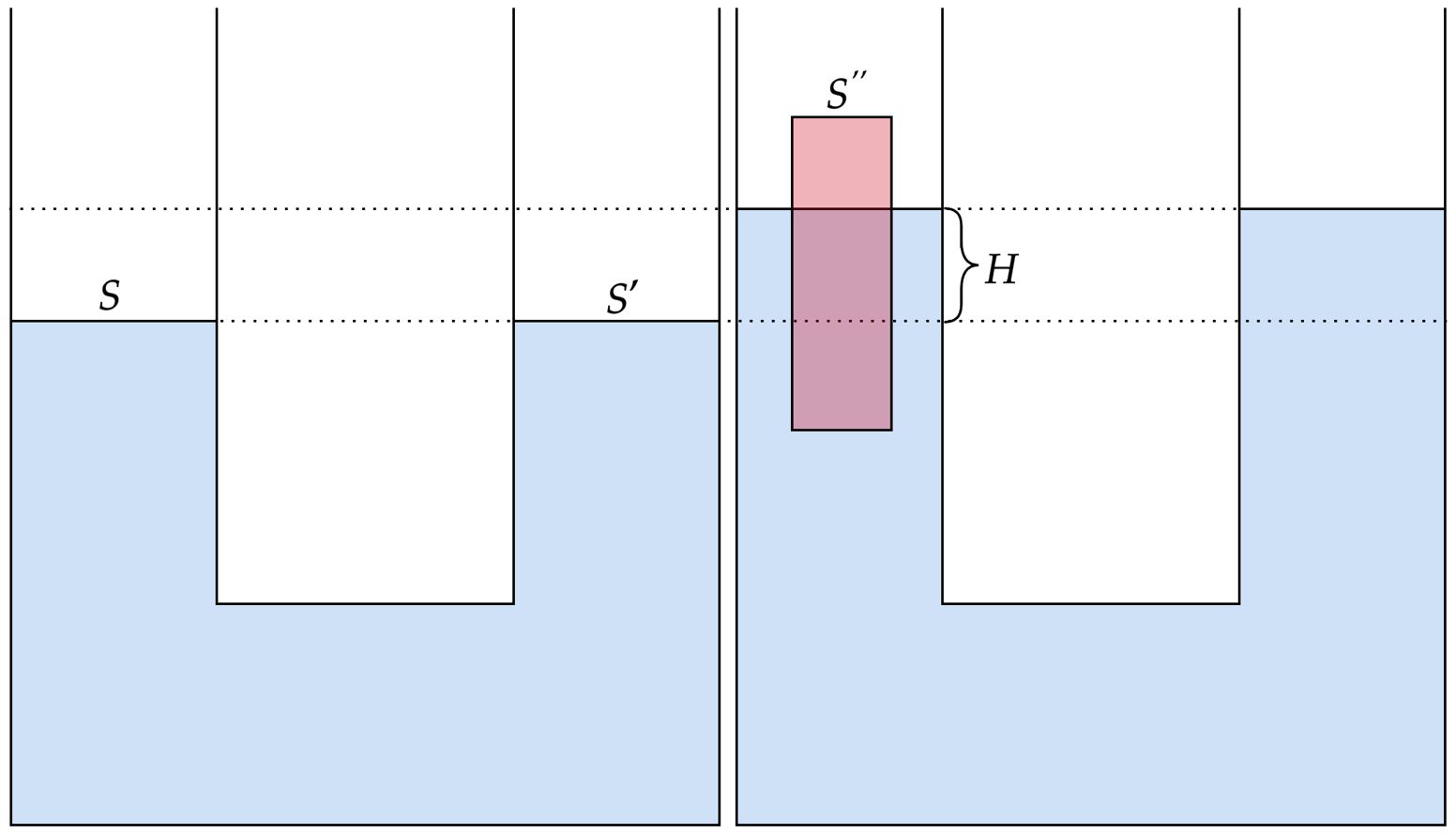 Com conhecimento do $\text{Princípio de Arquimedes}$, sabemos que o volume deslocado é igual ao volume submerso. Nesse contexto, podemos calcular esse volume deslocado $V_D$ como:\begin{matrix} V_D = H \cdot (S -S^{''} ) + H \cdot S^{'} &\therefore&V_D = H \cdot(S + S^{'}-S^{''})
\end{matrix}Pensando agora no equilíbrio do corpo, podemos escrever:\begin{matrix} E = P &\Rightarrow& \underbrace{ \rho_m \cdot g \cdot V_D}_{\text{Empuxo}} = \underbrace{\rho_F \cdot V \cdot g}_{\text{Peso}} &\therefore& H = \dfrac{\rho_F \cdot V}{\rho_m \cdot (S + S^{'} - S^{"})} & \tiny{\blacksquare}
\end{matrix}\begin{matrix}Letra \ (B)
\end{matrix}
Com conhecimento do $\text{Princípio de Arquimedes}$, sabemos que o volume deslocado é igual ao volume submerso. Nesse contexto, podemos calcular esse volume deslocado $V_D$ como:\begin{matrix} V_D = H \cdot (S -S^{''} ) + H \cdot S^{'} &\therefore&V_D = H \cdot(S + S^{'}-S^{''})
\end{matrix}Pensando agora no equilíbrio do corpo, podemos escrever:\begin{matrix} E = P &\Rightarrow& \underbrace{ \rho_m \cdot g \cdot V_D}_{\text{Empuxo}} = \underbrace{\rho_F \cdot V \cdot g}_{\text{Peso}} &\therefore& H = \dfrac{\rho_F \cdot V}{\rho_m \cdot (S + S^{'} - S^{"})} & \tiny{\blacksquare}
\end{matrix}\begin{matrix}Letra \ (B)
\end{matrix}

Ampliar Imagem

