Seja definida por: Se é um subconjunto não vazio de tal que é injetora, então:
Notação: $f(D) = {y \in \mathbb{R}: y = f(x), x \in D}$ e $\ln x$ denota o
logaritmo neperiano de x.
Observação: esta questão pode ser resolvida graficamente.
CossenoGPT
Teste gratuitamente agora mesmo! 
Observe o gráfico de $f$
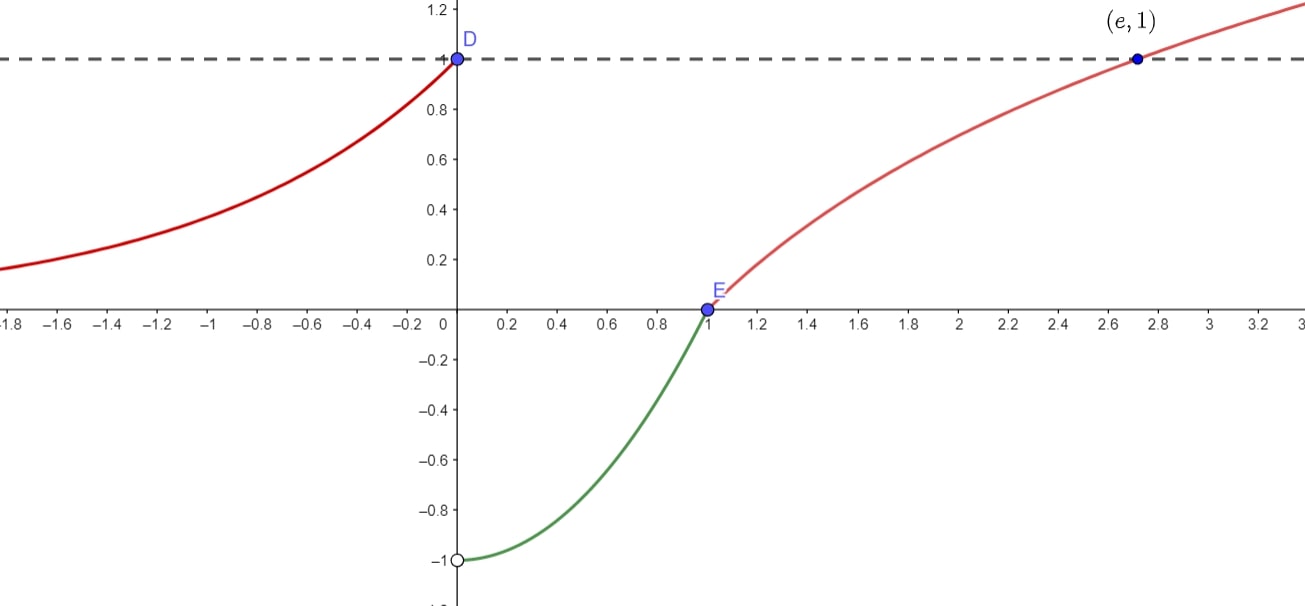Iremos analisar as opções:
$Letra \ A:$ Esta opção está errada, pois se $D = \mathbb{R}$ a função não será injetora, já que uma infinidade de pontos do ramo $e^x$ possui mesma imagem que uma infinidade de pontos do ramo $\ln{x}, 1 < x < e$
$Letra \ B:$ Esta opção está correta.
$Letra \ C:$ Esta opção está errada, pois $x = 0$ e $x = e$ possuem mesma imagem e, portanto, $f$ não é injetora.
$Letra \ D:$ Esta opção está errada pelo mesmo motivo da $Letra \ C$.
$Letra \ E:$ Errado, pois a $Letra \ B$ satisfaz
Ampliar Imagem
