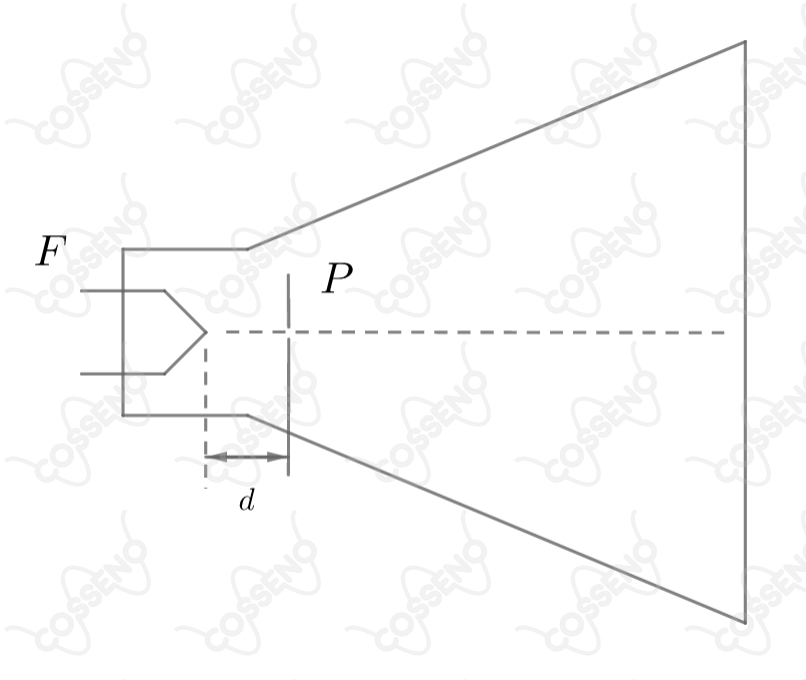
Num tubo de raios catódicos tem-se um filamento que libera elétrons quando aquecido, e uma placa aceleradora que é mantida num potencial mais alto que o filamento. O filamento fica a uma distância da placa. A placa tem, ainda, um orifício que permite a passagem dos elétrons que vão se chocar com uma tela que fluoresce quando os mesmos a atingem. Nestas condições:
CossenoGPT
Teste
gratuitamente agora
mesmo! 

Pelo $\text{Teorema do Trabalho Total}$, temos:
\begin{matrix} W_{fe} = \Delta E_c &\Rightarrow& e.\Delta V = E_{c_f}
\end{matrix} $\color{orangered}{Obs:}$ \begin{matrix} e: \text{carga elétrica} && \Delta V: \text{ddp entre a placa e o filamento} && E_{c_f}: \text{Energia cinética adquirida}
\end{matrix}
$• \ \text{Alternativa (A):}$ $\color{orangered}{\text{Incorreta}}$
Perceba que $e$ e $\Delta V$ são constantes, assim, a energia cinética independe da variação da distância. Nesse contexto, vale ressaltar que $\Delta V = E.d$, ao variar $d$, varia-se o campo elétrico também, sendo assim $\Delta V = cte$.
$• \ \text{Alternativa (B):}$ $\color{orangered}{\text{Incorreta}}$
Vide alternativa anterior.
$• \ \text{Alternativa (C):}$ $\color{royalblue}{\text{Correta}}$
Com conhecimento da explicação anterior, sabemos que ao variar $\Delta V$ devidamente iremos alterar a energia cinética.
$• \ \text{Alternativa (D):}$ $\color{orangered}{\text{Incorreta}}$
Vide alternativas anteriores.
$• \ \text{Alternativa (E):}$ $\color{orangered}{\text{Incorreta}}$
A $(C)$ está correta.
\begin{matrix} Letra \ (C)
\end{matrix}

