Uma bolinha de massa está oscilando livremente com movimento harmônico simples vertical, sob a ação de uma mola de constante elastica . Sua amplitude de oscilação é . Num dado instante, traz-se um recipiente contendo um líquido viscoso e obriga-se a partícula a oscilar dentro desse líquido. Depois de um certo tempo, retira-se novamente o recipiente com o líquido e constata-se que a partícula tem velocidade dada pela expressão: , onde , e são constantes.
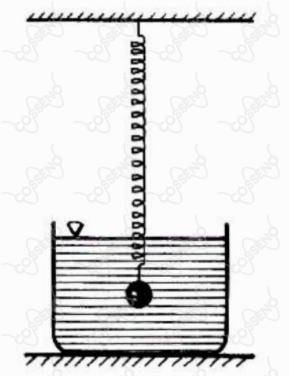
Desprezando as perdas de calor para o meio circundante e sabendo que o líquido tem capacidade calorífica , podemos afirmar que a variação de sua temperatura foi de:
CossenoGPT
Teste
gratuitamente agora
mesmo! 

Essa questão se resume em uma conservação de energia um pouco diferente do usual, pois parte da energia do corpo será cedido como forma de calor para o líquido.
$1)$ O corpo inicialmente está oscilando livremente, portanto, sua energia mecânica é dada por
$$E = \dfrac{kA^{2}}{2}.$$
$2)$ Quando o corpo entre em contato com a água, ele será forçado a oscilar dentro desse líquido viscoso, porém, sua oscilação será diferente, pois como o líquido é viscoso, parte de sua energia será cedida ao líquido na forma de calor, então sua energia mecânica será dada por
$$E = Q + \dfrac{mv^{2}_{0}}{2}.$$
Algumas considerações: a primeira é que veja que temos o calor envolvido na equação e a segunda é que o referencial está sendo adotado no ponto de velocidade máxima, portanto não há energia potencial e a velocidade considerada é $v_{0}$. Com isso, vale que
$$\dfrac{kA^{2}}{2} = Q + \dfrac{mv^{2}_{0}}{2} \Rightarrow \Delta \theta = \dfrac{1}{2C}\left(kA^{2} - mv^{2}\right).$$

