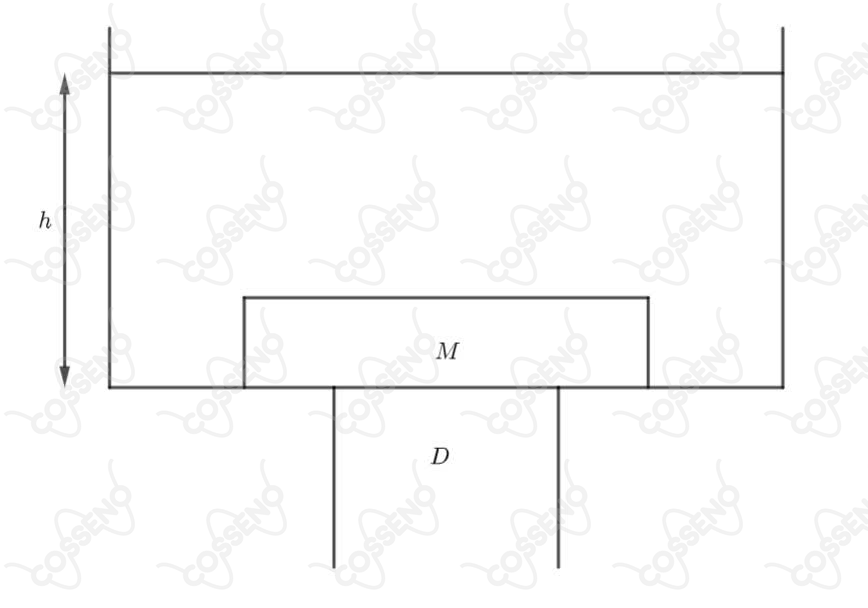
Na figura abaixo temos uma pia com um dreno . é um pedaço de madeira, de forma cilíndrica, que se apoia no fundo da pia em perfeito contato, de modo a tapar o dreno. Nestas condições, veda o dreno,
CossenoGPT
Teste
gratuitamente agora
mesmo! 

Neste caso, como o corpo como um todo não está em contato com a água (há uma parte em contato com a superfície e outra parte em contato com o ar) não podemos usar a expressão usual do empuxo para computar a força que o líquido exerce no bloco.
Observe que que podemos calcular a força que exercida na superfície inferior e superior do bloco de forma separada:
Inferior: $F_i = f + P_{atm} \cdot S_i$, onde $f$ é a força de contato do bloco com o recipiente e $P_{atm} \cdot S_i$ é a força da pressão atmosférica na área $S_i$.
Superior: $F_s = (P_{atm} + \rho g h) \cdot S_s$, onde $\rho g h$ é o aumento de pressão devido ao nível do líquido (aqui fez-se uma aproximação ao se considerar a altura do bloco muito menor que $h$), e $S_s$ a área superior do bloco.
Observe que $S_s > S_i$. Assim, no caso limite em que o bloco se descola do fundo, teremos $F_i = P_{atm} \cdot S_i$ e $F_s = (P_{atm} + \rho g h) \cdot S_s$, onde obviamente $F_s > F_i$, portanto o bloco sempre vedará o fundo, para $h$ suficientemente grande

