UNICAMP 2011 Matemática - Questões

Um grupo de pessoas resolveu encomendar cachorros-quentes para o lanche. Entretanto, a lanchonete enviou apenas 15 sachês de mostarda e 17 de catchup, o que não é suficiente para que cada membro do grupo receba um sachê de cada molho. Desta forma, podemos considerar que há três subgrupos: um formado pelas pessoas que ganharão apenas um sachê de mostarda, outro por aquelas que ganharão apenas um sachê de catchup, e o terceiro pelas que receberão um sachê de cada molho.

1. a) Sabendo que, para que cada pessoa ganhe ao menos um sachê, 14 delas devem receber apenas um dos molhos, determine o número de pessoas do grupo.

2. b) Felizmente, somente 19 pessoas desse grupo quiseram usar os molhos. Assim, os sachês serão distribuídos aleatoriamente entre essas pessoas, de modo que cada uma receba ao menos um sachê. Nesse caso, determine a probabilidade de que uma pessoa receba um sachê de cada molho.

No mês corrente, uma empresa registrou uma receita de R$ $600$ mil e uma despesa de R$ $800$ mil. A empresa estuda, agora, alternativas para voltar a ter lucro.

1. a) Primeiramente, assuma que a receita não variará nos próximos meses, e que as despesas serão reduzidas mensalmente, em exatos R$ 45 mil. Escreva a expressão do termo geral da progressão aritmética que fornece o valor da despesa em função de $n$, o número de meses transcorridos, considerando como mês inicial o corrente. Calcule em quantos meses a despesa será menor que a receita.
   

2. b) Suponha, agora, que a receita aumentará 10% a cada mês, ou seja, que a receita obedecerá a uma progressão geométrica (P.G.) de razão 11/10. Nesse caso, escreva a expressão do termo geral dessa P.G. em função de $\mathbf{n}$, o número de meses transcorridos, considerando como mês inicial o corrente. Determine qual será a receita acumulada em 10 meses. Se necessário, use ${1,1}^2=1,21;{\ \ 1,1}^3\approx 1,33\ \ e\ \ {1,1}^5\approx 1,61$.
   

Recentemente, um órgão governamental de pesquisa divulgou que, entre $2006$ e $2009$, cerca de $5,2$ milhões de brasileiros saíram da condição de indigência. Nesse mesmo período, $8,2$ milhões de brasileiros deixaram a condição de pobreza. Observe que a faixa de pobreza inclui os indigentes. O gráfico abaixo mostra os percentuais da população brasileira enquadrados nessas duas categorias, em $2006$ e $2009$.

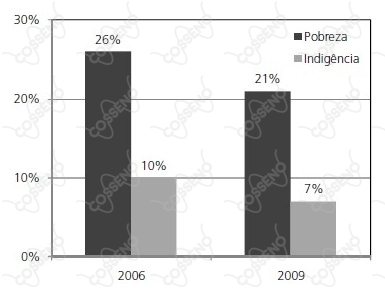
Após determinar a população brasileira em $2006$ e em $2009$, resolvendo um sistema linear, verifica-se que

Para certo modelo de computadores produzidos por uma empresa, o percentual dos processadores que apresentam falhas após $T$ anos de uso é dado pela seguinte função: $$P\left(T\right)=100(1-2^{-0,1T})$$

1. a) Em quanto tempo 75% dos processadores de um lote desse modelo de computadores terão apresentado falhas?

2. b) Os novos computadores dessa empresa vêm com um processador menos suscetível a falhas. Para o modelo mais recente, embora o percentual de processadores que apresentam falhas também seja dado por uma função na forma $Q\left(T\right)=100(1-2^{cT})$, o percentual de processadores defeituosos após 10 anos de uso equivale a $1/4$ do valor observado, nesse mesmo período, para o modelo antigo (ou seja, o valor obtido empregando-se a função P(T) acima). Determine, nesse caso, o valor da constante c. Se necessário, utilize ${{{\log}}_2 (7)\approx 2,81\ }$.

Considere três modelos de televisores de tela plana, cujas dimensões aproximadas são fornecidas na tabela abaixo, acompanhadas dos preços dos aparelhos.

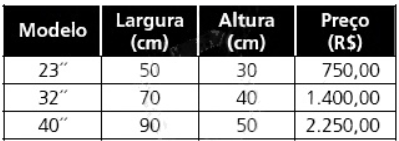
Com base na tabela, pode-se afirmar que o preço por unidade de área da tela: