UNB 2022 - Questões

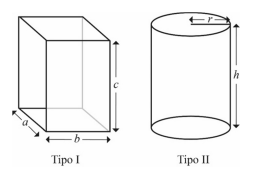
As figuras anteriores ilustram os dois formatos de embalagens de papelão que uma empresa confecciona em variados tamanhos. Considerando que, em todas as situações, as caixas estão fechadas, desconsiderando as bordas do material deixadas nas extremidades para a colagem das caixas e assumindo 3,14 como o valor aproximado de π, julgue o item a seguir.

Uma embalagem com formato do tipo II com raio de 8 cm e capacidade para 1 litro deve ter altura superior a 5 cm.

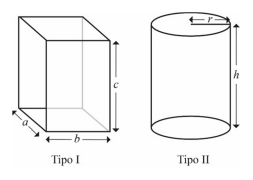
As figuras anteriores ilustram os dois formatos de embalagens de papelão que uma empresa confecciona em variados tamanhos. Considerando que, em todas as situações, as caixas estão fechadas, desconsiderando as bordas do material deixadas nas extremidades para a colagem das caixas e assumindo 3,14 como o valor aproximado de π, julgue o item a seguir.

Para uma embalagem do tipo II, se o raio for duplicado e a altura for mantida, então o volume também será duplicado.

Considerando que, na unidade de pronto-socorro de um hospital, quatro médicos façam atendimento aos pacientes e que haja a mesma probabilidade de esses pacientes serem atendidos por qualquer um desses médicos.

Considere que a quantidade de dias semanais em que cada um dos médicos atende no pronto socorro corresponda, respectivamente, a cada uma das raízes reais do polinômio p(x) = (x-2).(x³ - 6x² + 11x - 6)

Nesse caso, se, nos dias de atendimento, cada um dos médicos atender durante 6 horas, então a quantidade total de horas semanais disponibilizadas pelos quatro médicos será superior a 40 horas.

Uma matriz em duas dimensõesA_{2 ×2} é uma matriz de rotação quando a multiplicação de um par ordenado V(x, y) na forma de matriz coluna $V=\left[\begin{matrix}x\\z\end{matrix}\right]$ por A produz como resultado um vetor $V_1=\left[\begin{matrix}x_1\\z_1\end{matrix}\right],$ que pode ser identificado com o par ordenado $V_1\left(x_1,y_1\right)$ cuja distância à origem é a mesma que V. Nesse contexto, seja a matriz A abaixo, em que a ∈ℝ.

Considere que a matriz A faça uma rotação por um ângulo α em um ponto P(x, y) do plano, na seguinte forma.

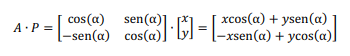
Então $P_1$ (xcos (α) + ysen(α), - xsen (α) + ycos (α)) é o ponto obtido de pela rotação de P, em torno da origem, por um ângulo α

Tendo como referência essas informações, julgue o item.

Se $A=\left[\begin{matrix}\frac{\sqrt{3}}{2}&\frac{1}{2}\\-\frac{1}{2}&\frac{\sqrt{3}}{2}\end{matrix}\right],$ então o ponto $P_1\left(4,0\right)$ é obtido pela rotação através da matriz A de um ponto P(x, y) al que $ x = 2.$

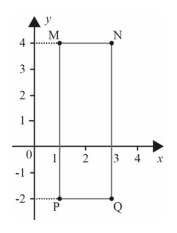
No sistema de coordenadas xOy a seguir, foi traçado o retângulo de vértices $M(1,4),N(3,4),P(1,-2),Q(3,-2).$

Nesse sistema, para fazer a rotação de um segmento CD, por exemplo, é suficiente fazer a rotação dos extremos C e D do segmento dado.

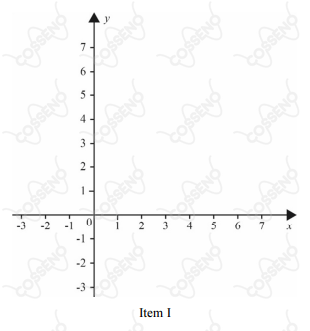
Com base nessas informações, faça o que se pede nos itens I e II a seguir, utilizando os sistemas de coordenadas disponibilizados.

I Trace o efeito da rotação no retângulo, a partir da matriz A, para $\alpha=\frac{\pi}{2}.$

II Trace o efeito da rotação no retângulo, a partir da matriz $\sqrt{2}\cdot A,$ para $\alpha=-\frac{\pi}{4}.$