Uma matriz em duas dimensõesA_{2 ×2} é uma matriz de rotação quando a multiplicação de um par ordenado V(x, y) na forma de matriz coluna $V=\left[\begin{array}{c}x\\ z\end{array}\right]$ por A produz como resultado um vetor $V_1=\left[\begin{array}{c}{x}_1\\ z_1\end{array}\right],$ que pode ser identificado com o par ordenado $V_1\left(x_1,y_1\right)$ cuja distância à origem é a mesma que V. Nesse contexto, seja a matriz A abaixo, em que a ∈ℝ.

Considere que a matriz A faça uma rotação por um ângulo α em um ponto P(x, y) do plano, na seguinte forma.

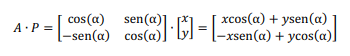
Então $P_1$ (xcos (α) + ysen(α), - xsen (α) + ycos (α)) é o ponto obtido de pela rotação de P, em torno da origem, por um ângulo α

Tendo como referência essas informações, julgue o item.

Se $A=\left[\begin{array}{cc}\frac{\sqrt{3}}{2}& \frac{1}{2}\\ -\frac{1}{2}& \frac{\sqrt{3}}{2}\end{array}\right],$ então o ponto $P_1\left(4,0\right)$ é obtido pela rotação através da matriz A de um ponto P(x, y) al que $x=2.$