UERJ 2013 Matemática - Questões

Um imóvel perde 36% do valor de venda a cada dois anos. O valor $V\left(t\right)$ desse imóvel em $t$ anos pode ser obtido por meio da fórmula a seguir, na qual $V_{0}$ corresponde ao seu valor atual. $$V\left(t\right)=V_{0} \times \left(0,64\right)^{\frac{t}{2} }$$ Admitindo que o valor de venda atual do imóvel seja igual a 50 mil reais, calcule seu valor de venda daqui a três anos.

Um professor propõe a um aluno uma tarefa de matemática composta das etapas descritas a seguir.

1ª Escrever o número de quatro algarismos da data de seu aniversário, dois referentes ao dia e dois referentes ao mês.

2ª Misturar os quatro algarismos desse número formando um número $N$, de modo que a ordem das unidades de milhar não seja ocupada por zero.

3ª Subtrair 1001 do número $N$, tantas vezes quantas forem necessárias, até obter o primeiro valor menor do que 1001.

4ª Informar ao professor o valor obtido na 3ª etapa.

5ª Calcular o resto $R$ da divisão do número $N$, obtido na 2ª etapa, por 11.

O professor consegue determinar o valor de $R$ sem conhecer o valor de $N$.

Sabendo que o valor obtido na 3ª etapa foi 204, determine $R$.

Em uma atividade escolar, qualquer número $X$, inteiro e positivo, é submetido aos procedimentos matemáticos descritos abaixo, quantas vezes forem necessárias, até que se obtenha como resultado final o número 1.

$$\text{Se}\ X \ \text{é múltiplo de 3, deve-se dividi-lo por 3.}$$

$$\text{Se} \ X \ \text{não é divisível por 3, deve-se calcular} \ X-1.$$

A partir de $X=11$, por exemplo, os procedimentos são aplicados quatro vezes. Veja a sequência dos resultados obtidos:

Iniciando-se com $X=43$, o número de vezes que os procedimentos são utilizados é igual a:

Em um laboratório, duas torneiras enchem dois recipientes, de mesmo volume $V$, com diferentes soluções aquosas. Observe os dados da tabela:

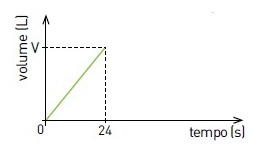
O gráfico abaixo mostra a variação do volume do conteúdo em cada recipiente em função do tempo.

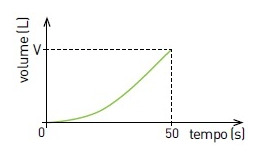
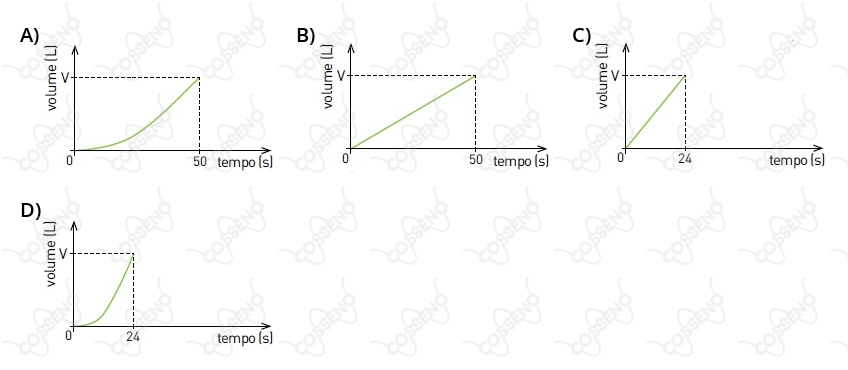
O gráfico que ilustra a variação do volume do conteúdo desse recipiente está apresentado em:

Um lago usado para abastecer uma cidade foi contaminado após um acidente industrial, atingindo o nível de toxidez $T_{0}$,correspondente a dez vezes o nível inicial.

Leia as informações a seguir.

• A vazão natural do lago permite que 50% de seu volume sejam renovados a cada dez dias.

• O nível de toxidez $T\left(x\right)$, após $x$ dias do acidente, pode ser calculado por meio da seguinte equação: $$T\left(x\right)=T_{0} \cdot \left(0,5\right)^{0,1\ x}$$

Considere $D$ o menor número de dias de suspensão do abastecimento de água, necessário para que a toxidez retorne ao nível inicial.

Sendo $\log\ 2=0,3$, o valor de $D$ é igual a: