UEL 2020 Matemática - Questões
Abrir Opções Avançadas
Na exposição virtual “A Beleza da Matemática”, realizada no Museu do Amanhã, o belo é celebrado como simetria matemática, como exemplificado na imagem a seguir.

Imagem da exposição “A Beleza da Matemática” , Museu do Amanhã
No plano cartesiano, dois pontos distintos $P$ e $Q$ são simétricos em relação a uma reta $r$ se as seguintes condições forem simultaneamente atendidas:
I. a distância de $P$ a $r$ é igual à distância de $Q$ a $r$.
II. a reta que contém $P$ e $Q$ é perpendicular à reta $r$.
Suponha que, no plano que contém a imagem da borboleta, o eixo de simetria $r$ seja dado pela equação de reta $y + x = 2$. Se $P = (-2, 0)$ é um ponto desse plano, assinale a alternativa que apresenta, corretamente, o ponto simétrico a $P$ em relação à reta $r$.
Uma característica fundamental do plano corpóreo de um animal é sua forma geral e um aspecto básico dessa forma é a simetria. O termo simetria refere-se ao arranjo regular das estruturas corporais em relação ao eixo do corpo. Os animais que podem ser divididos ao longo de ao menos um plano, de modo que as metades resultantes sejam semelhantes entre si, são conhecidos como simétricos.
Com base nas informações apresentadas, considere as afirmativas a seguir.
I. Um corpo com simetria bilateral tem a forma geral de um cilindro, com um eixo principal ao redor do qual as diversas partes do corpo estão dispostas.
II. Na simetria bilateral, um lado do corpo difere do outro por uma escala distinta de 1, fazendo com que as áreas, em cada lado, se alterem nessa mesma escala.
III. É vantajoso para um animal com simetria radial, pelo seu estilo de vida, ser capaz de interagir com o ambiente igualmente a partir de várias direções.
IV. O volume do corpo de um animal, que admite simetria bilateral exata, é igual ao dobro do volume de qualquer um de seus dois lados.
Assinale a alternativa correta.
A icônica obra Mona Lisa, de Leonardo Da Vinci, exposta no Museu do Louvre, possibilita pôr à prova as proporções matemáticas nela presentes. Partindo de um quadrado $ABCD$ de lado $1$, que delimita uma região abaixo da cabeça, pode-se obter um retângulo, que contém a cabeça da Mona Lisa, por meio da construção geométrica descrita a seguir.
Seja $O$ o ponto médio do segmento $\overline{\text{AB}}$. Tome a circunferência de centro $O$ e raio $\overline{\text{OB}}$. Encontre o ponto $E$ dado pela intersecção da circunferência com a semirreta $\overrightarrow{\text{BA}}$. Considere o ponto $F$ de modo a obter o retângulo de vértices $EADF$, como ilustrado na figura a seguir.
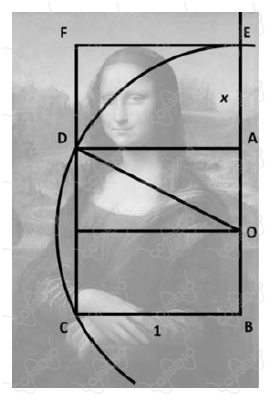
Com base na construção geométrica fornecida e na figura, assinale a alternativa que apresenta, corretamente, o comprimento do segmento $\overline{\text{EA}}$.
Leia o texto e observe a imagem a seguir.
No Brasil, a preservação natural de um cadáver é rara devido ao clima tropical e ao solo ácido, que aceleram a sua decomposição. Por isso, a múmia encontrada em Goianá, Minas Gerais, no século XIX é tão incomum.
Passados $t$ anos após a morte deste ser humano, suponha que a massa $m(t)$ de seu cadáver, medida em quilogramas, seja dada por $m(t) = 40e^{-C\cdot t}$, onde $e > 1$ é uma constante e $C$ é um parâmetro relacionado às características morfoclimáticas da região onde originalmente se encontrava. Admitindo que passados $t = 600\ \text{anos}$ a múmia possuía exatos $4\ \text{kg}$, assinale a alternativa que apresenta, corretamente, o valor do parâmetro $C$.
Leia o texto a seguir.
Luzia é de inestimável valor científico por se tratar do mais antigo fóssil humano paleoamericano já encontrado no Brasil. O crânio e ossos da coxa e do quadril de Luzia foram achados em $1975$, em uma gruta da região de Lagoa Santa, em Minas Gerais. Seu esqueleto foi datado de $11,5$ mil anos e ela deve ter morrido aos $25$ anos. Neste século, seu rosto foi reconstituído na Inglaterra.
Adaptado de: www.museunacional.ufrj.br
Um dos processos de datação arqueológica ocorre calculando o porcentual $r$ da quantidade de carbono $14$ presente no fóssil em relação à quantidade desse mesmo elemento encontrada em um ser vivo de características semelhantes. Suponha que para fósseis humanos paleoamericanos a figura a seguir exiba o gráfico da função $f : {\mathbb{R}_+^*} + \rightarrow \ \mathbb{R}_+$ que associa, a cada $r$, a quantidade $t = f(r)$ de anos que se passaram desde a morte do ser humano em questão.
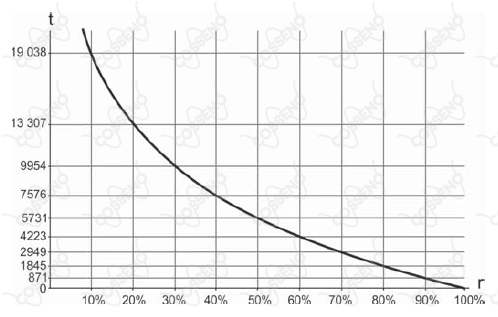
Com base no texto e no gráfico, assinale a alternativa correta.
Carregando...