UEL 2017 - Questões

Com a finalidade de se calcular a quantidade de pessoas presentes em manifestações sociais em determinado trecho urbano, são utilizadas diferentes metodologias, sendo que uma delas consiste em quatro etapas:

1. estabelece-se a área $A$ (em $\text{m}^2$) da região delimitada pelo trecho da manifestação;

2. posicionam-se alguns fiscais que ficam responsáveis, cada um, por uma sub-região fixa e exclusiva do trecho urbano, a fim de coletar, de maneira simultânea e periódica, quantas pessoas se encontram em sua sub-região no momento de cada medição;

3. calcula-se a média $M$ de todas as medições realizadas por todos os fiscais;

4. ao final, declara-se que há $A\cdot M$ pessoas presentes na manifestação.

Suponha que uma manifestação ocorreu na região hachurada dada pelo setor de uma coroa circular de centro $O$ (conforme figura) e que foi observada por 3 medições com 2 fiscais cada, cujas tabelas dos dados coletados encontram-se a seguir.

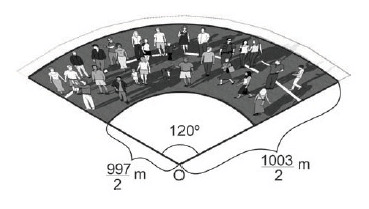
Considerando essa metodologia e a aproximação $\pi\approx\dfrac{22}{7}$, assinale a alternativa que apresenta, corretamente, a quantidade de pessoas que estiveram presentes na manifestação, naquele trecho.

(Alex Flemming, Estação Sumaré, instalação, fotografias e textos impressos com tinta vinílica sobre vidro, 44 peças de 1,75 m $\times$ 1,25 m cada, 1998.)

Leia o texto a seguir.

A biometria é utilizada para a identificação pessoal e apresenta as seguintes características: universalidade, imutabilidade, facilidade de coleta e aceitação pública. A utilização das impressões digitais para reconhecimento biométrico oferece segurança e eficácia, podendo substituir os cartões e as senhas que se usa no dia a dia.

(Adaptado de: MAZI, R. C.; PINO JUNIOR, A. Identificação biométrica através da impressão digital usando redes neurais artificiais. Anais do XIV Encita. 2008.)

Suponha que esse processo seja constituído de duas etapas: na primeira, o usuário tem seu polegar digitalizado e a imagem gerada é transformada em um padrão matemático; na segunda, esse padrão é comparado em um banco de dados de usuários para se determinar a quem pertence a imagem digitalizada.

Suponha também que o padrão matemático armazenado seja a equação da elipse central presente no polegar direito e que o banco de dados de usuários contenha as entradas a seguir.

Um desses usuários teve o polegar direito digitalizado e as propriedades da elipse central E (ilustrada na figura) são as seguintes:

• A elipse $E$ passa pelo ponto $(1,\ 0)$;

• A elipse $E$ não intercepta o eixo $y$;

• A elipse $E$ intercepta o eixo $x$ em apenas um ponto.

Assinale a alternativa que apresenta, corretamente, o usuário a quem pertence a digital.

Leia o texto a seguir.

Precisamos de um nome para o novo replicador, um substantivo que comunique a ideia de unidade de transmissão cultural. “Mimeme” vem do grego “aquilo que é replicado”, mas eu quero um monossílabo que se pareça com gene. Eu espero que meus amigos clássicos me perdoem por abreviar mimeme para meme. Se uma ideia se alastra, é dita que se propaga sozinha.

(Adaptado de: DAWKINS, R. O gene egoísta. Trad. Geraldo H. M. Florsheim. Belo Horizonte: Itatiaia, 2001. p.214.)

Diversos segmentos têm utilizado serviços de marketing para criação e difusão de memes de seu interesse. Um partido político com $P_0 = 20$ filiados encomendou um anúncio que se tornou um meme em uma rede social, sendo que 5% dos $K = 2\cdot 10^9$ usuários ativos visualizaram o anúncio no instante $t = 1$. Sejam $e > 1$, $r > 0$ constantes e suponha que a função $P(t)$ dada por

$$P(t) = \dfrac{K\cdot P_0\cdot e^{r\cdot t}}{K + P_0\left(e^{r\cdot t} - 1\right)}$$

representa a quantidade de usuários da rede social que visualizaram o meme no instante $t$.

Assinale a alternativa que apresenta, corretamente, o valor da constante $r$ para essa rede social.

(Disponível em: . Acesso em: 27 abr. 2016.)

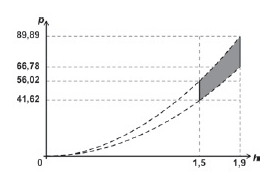
Existem critérios, cada qual com suas vantagens e limitações, para determinar se certo indivíduo é obeso. Um dos principais testes aplicados para esse fim é o cálculo do Índice de Massa Corporal (IMC), definido pela equação

$$I=\dfrac{p}{h^2}$$

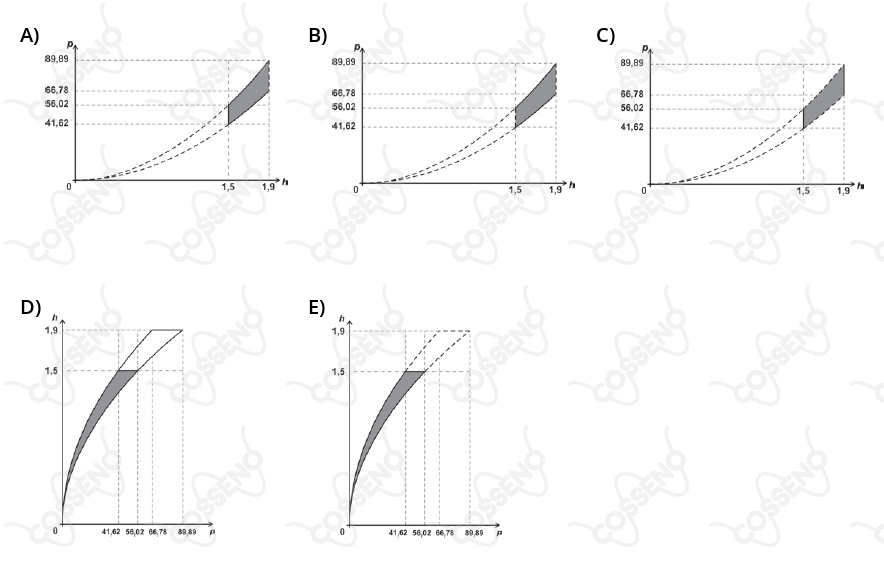
em que $I$ representa o IMC $\left(\text{kg/m}^2\right)$, $h$ representa a altura $(\text{m})$ e $p$ representa a massa $\left(kg\right)$. De acordo com a Organização Mundial da Saúde (OMS), um indivíduo é classificado como tendo IMC normal se $18,5\leq I\leq 24,9$. Considerando um universo composto por indivíduos adultos, cuja altura $h$ seja tal que $1,5\leq h < 1,9$, assinale a alternativa que apresenta, corretamente, a região no plano cartesiano $h\times p$ definida por todas as combinações de altura e massa dos indivíduos com IMC normal, nesse universo.

(Disponível em: . Acesso em: 27 abr. 2016.)

Leia o texto a seguir.

Por que não dividir um segmento unitário em duas partes iguais? A resposta é que, simplesmente, com a igualdade não existe diferença, e sem diferença não há universo perceptivo. O “número de ouro” é uma razão constante derivada de uma relação geométrica que os antigos chamavam de “áurea” ou de divisão perfeita, e os cristãos relacionaram este símbolo proporcional com o Filho de Deus.

(Adaptado de: LAWLOR, R. Mitos – Deuses – Mistérios – Geometria Sagrada. Madrid: Edições del Prado, 1996. p.46.)

O número de ouro, denotado pela letra grega $\phi$, é definido como a única raiz positiva da equação a seguir.

$$x^2=x+1$$

Com base no texto e na definição do número de ouro, atribua V (verdadeiro) ou F (falso) às afirmativas a seguir.

($\quad$) $2\phi=1+\sqrt{5}$ ($\quad$) O número de ouro $\phi$ pode ser expresso como um quociente de números inteiros não nulos. ($\quad$) Os números $\phi$, $\phi + 1$, $2\phi + 1$ estão em progressão geométrica de razão $\phi$. ($\quad$) $\phi^{-1}=\phi-1$
($\quad$) $\phi$ não pode ser expresso através de uma equação, por ser derivado de uma relação geométrica.

Assinale a alternativa que contém, de cima para baixo, a sequência correta.