UEL 2016 Matemática - Questões

Figura 1: Eduardo Kac, GFP Bunny, 2000

Leia o texto a seguir.

Câncer é essencialmente caracterizado pelo crescimento desordenado de células que invadem órgãos e tecidos, sendo considerado atualmente um sério problema de saúde pública mundial. Sabe-se que as células tumorais competem entre si por recursos vitais e oxigênio. Um modelo de crescimento tumoral é descrito pela função

$$N(t) = \dfrac{k}{1+\left(\dfrac{k}{N_0} -1\right) \cdot (2,7)^{-rt}}$$

que determina, a cada instante $t$, a população de células cancerígenas; sendo que $r$ é a constante de crescimento intrínseca dessas células, $N_0$ é a população inicial de células tumorais; $K$ é a maior quantidade de células que um tumor maligno pode atingir com os nutrientes disponíveis.

(Adaptado de: RODRIGUES, D. S. Modelagem Matemática em Câncer: dinâmica angiogênica e quimioterapia anti-neoplásica. Dissertação de Mestrado. Universidade Paulista “Júlio de Mesquita Filho”, 2011. p.13.)

A partir dessas informações, atribua V (verdadeiro) ou F (falso) às afirmativas a seguir.

($\quad$) Se $t = 0$, então $N(t) = N_0$.

($\quad$) $K$ pode assumir valores negativos.

($\quad$) $N_0$ é sempre maior que $K$.

($\quad$) Se $N_0 = K$, então $N(t) = K$.

($\quad$) Quando $t$ cresce ilimitadamente, $(2, 7)^{-rt}$ se aproxima de $0$ (zero) e $N(t)$ é aproximadamente $K$.

Assinale a alternativa que contém, de cima para baixo, a sequência correta.

A meia-vida de um elemento radioativo é o tempo necessário para que sua atividade seja reduzida à metade da atividade inicial, ou seja, o elemento radioativo perde metade de sua massa a cada período de tempo. A braquiterapia é uma das modalidades de tratamento da radioterapia contra o câncer, e um dos elementos radioativos utilizados é o $\ ^{103}Pd$, cuja meia-vida é de 17 dias. Considerando a massa inicial de 16 g de $\ ^{103}Pd$, assinale a alternativa que apresenta, corretamente, a massa desse elemento radioativo decorridos 136 dias.

Um dos principais impactos das mudanças ambientais globais é o aumento da frequência e da intensidade de fenômenos extremos, que quando atingem áreas ou regiões habitadas pelo homem, causam danos. Responsáveis por perdas significativas de caráter social, econômico e ambiental, os desastres naturais são geralmente associados a terremotos, tsunamis, erupções vulcânicas, furacões, tornados, temporais, estiagens severas, ondas de calor etc.

(Disponível em: . Acesso em: 20 maio 2015.)

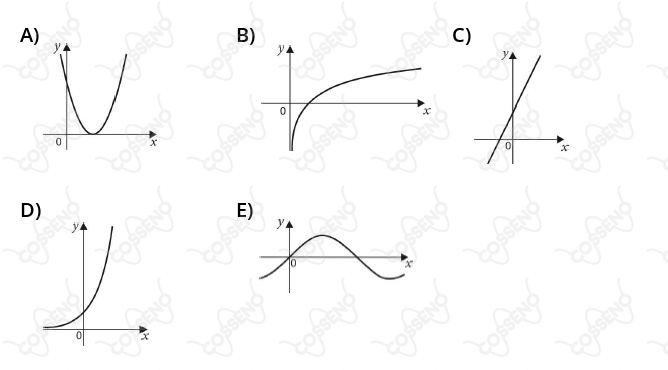
Em relação aos tremores de terra, a escala Richter atribui um número para quantificar sua magnitude. Por exemplo, o terremoto no Nepal, em 12 de maio de 2015, teve magnitude 7,1 graus nessa escala. Sabendo-se que a magnitude $y$ de um terremoto pode ser descrita por uma função logarítmica, na qual $x$ representa a energia liberada pelo terremoto, em quilowatts-hora, assinale a alternativa que indica, corretamente, o gráfico dessa função.

Leia o texto a seguir.

Segundo teorias demográficas, a população mundial cresceria em ritmo rápido, comparado a uma PG = ($2, 4, 8, 16, 32, 64, \dots , a_t, ...$), e a produção mundial de alimentos cresceria em um ritmo lento, comparado a uma PA = ($1, 2, 3, 4, \dots , b_t, ...$).

(Adaptado de: $<$http://educação.uol.com.br/disciplinas/geografia/teorias-demograficas-malthusianos-neomalthusianos-e-reformistas.htm$>$. Acesso em: 15 jun. 2015.)

Suponha que PA seja a sequência que representa a quantidade de alimentos, em toneladas, produzidos no tempo $t > 0$, e que PG seja a sequência que representa o número de habitantes de uma determinada região, nesse mesmo tempo t. A partir dessas informações, assinale a alternativa que apresenta, corretamente, a razão entre a quantidade de alimentos, em $\text{kg}$, e o número de habitantes, para $t = 10\ \text{anos}$.