PUC-SP 2017 - Questões

A figura mostra um triângulo retângulo $ABC$, de hipotenusa $\overline{AC}$, com $A(2,7), B(7,2)$ e $C(k, k-5)$

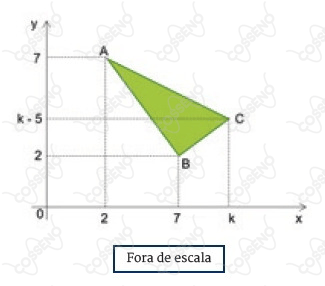
Sabendo que a área do triângulo $ABC$ é $15 \ cm^2$, o valor da abscissa do ponto $C$ é

Uma senha é formada por quatro algarismos distintos $ABCD$ que obedecem às seguintes condições:

1. 1) $A + B + C + D = 11$
   

2. 2) $A \cdot B \cdot C = 30$
   

3. 3) $A + B = C$
   

4. 4) $A \cdot B = C + D$
   

Sabendo que $A < B$, o valor de $A + C$ é

Considere o retângulo $ABCD$, com $\overline{AB} = 8 \ cm$, $\overline{BC} = 5 \ cm$ e o segmento $\overline{PS}$ que intersecta os prolongamentos dos lados $\overline{AD}$ e $\overline{BC}$ nos pontos $P$ e $S$, respectivamente, conforme mostra a figura.

Sabendo que $\overline{AP} = 3 \ cm$ e $\overline{CS} = 2 \ cm$, a área do quadrilátero $QBCR$ é

Um bloco maciço de madeira na forma de um prisma reto de base retangular medindo $18 \ cm$ por $24 \ cm$ e com $30 \ cm$ de altura, foi totalmente dividido em cubinhos iguais e de maior aresta possível.

Supondo que não tenha ocorrido perda alguma no corte do bloco, o volume de um cubinho é

Um número é chamado “perfeito” se ele for igual à soma de seus divisores, excluindo ele mesmo.

Se $S = 2^n – 1$ é um número primo, então o número $P=2^{n - 1} \cdot S$ será um número “perfeito”

Fonte: A Magia dos Números/ Paul Karlson. (Adaptado)

Sabendo que o número $496$ é um número “perfeito”, os valores de $n\ e\ S$ são, respectivamente