PUC-SP 2010 Matemática - Questões

Na tira abaixo, Zé Vampir e Penadinho aparecem disputando uma partida do conhecido “jogo da velha”. Desse jogo, participam duas pessoas que devem, alternada e sucessivamente, assinalar suas respectivas marcas em um esquema composto de $9$ casas. Vence a partida o jogador que primeiro conseguir preencher com a sua marca todas as casas de uma linha, coluna ou diagonal do esquema

O Estado de São Paulo. 25 abr. 2010.

Suponha que, apesar do medo que aparenta, Zé Vampir volta a jogar e assinala sua marca da forma como é mostrado na figura abaixo:

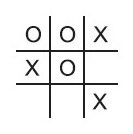
Nas alternativas que seguem, são apresentados esquemas de outras partidas que se encontram no mesmo estágio que a de Zé Vampir e Penadinho, ou seja, apresentam o mesmo número de jogadas.

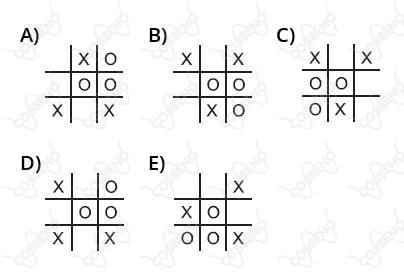
Desses esquemas, aquele em que a situação apresentada Não é equivalente à do esquema mostrado acima é

Sabe-se que em dezembro de $2007$ as indústrias $X$ e $Y$ produziram $6 000$ e $2 400$ unidades de um mesmo artigo, respectivamente. A partir de então, a cada mês subsequente, $X$ teve sua produção acrescida de $5\%$ da quantidade produzida em dezembro de $2007$, enquanto que, da mesma forma, $Y$ teve a sua acrescida em $20\%$ da quantidade produzida na mesma data. Nessas condições, é correto afirmar que a produção de tal artigo em $X$ foi superada pela sua produção em $Y$ a partir de

Relativamente a função quadrática $f$, dada por $f(x) = ax^2 + bx + c$, em que $a$, $b$ e $c$ são constantes reais, sabe-se que o valor mínimo é $-4$; seu gráfico tem o eixo da ordenadas como eixo de simetria e a a distância entre as raízes é $8$. Assim sendo, a equação da reta que contém o ponto $(a; c)$ e tem inclinação de $135^\circ$ é

No plano complexo, seja o triângulo cujos vértices $U$, $V$ e $W$ são respectivas imagens dos números complexos $u = 4 \cdot (\cos\ 60^\circ + i \cdot \hspace{2pt}\mathrm{sen}\ 60^\circ)^2$, $v = u \cdot i$ e $w = 4 \cdot i^{147}$. A área do triângulo $UVW$, em unidades de superfície, é

Em média, Alceste, Belizário e Cibele gastam $t_A$, $t_B$ e $t_C$ minutos, respectivamente, para encher um tanque inicialmente vazio e, para tal, só usam recipientes de iguais capacidades, totalmente cheios de água. Sabe-se também que a equação matricial

$$\left(\begin{array}{rclrcl} 1 && 1 && 0\\ 1 && 0 && 1\\ 0 && 1 &&1 \end{array}\right) \cdot \left(\begin{array}{c} t_A\\ t_B\\ t_C \end{array}\right) = \left(\begin{array}{c} 30\\ 25\\ 35 \end{array}\right)$$

permite que se calculem $t_A$, $t_B$ e $t_C$, em minutos, e que tal tanque tem a forma de um paralelepípedo retângulo de $3$ metros de altura. Nessas condições, após quantos minutos, em média, contados a partir do instante em que os três começarem simultaneamente a colocar água no tanque vazio, o nível da água atingirá $1,95\ m$ de altura?