PUC-RJ 2020 Física - Questões

Dois corpos estão ligados, como na figura, sendo a aceleração do sistema igual a $\frac{g}{10}$, onde $g$ é a aceleração da gravidade. O corpo $1$, que está pendente, tem massa $M$. O corpo $2$, que se move em uma mesa horizontal, tem massa $4M$.

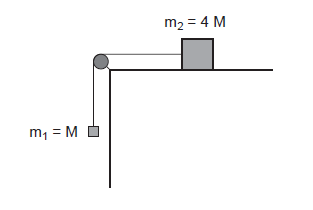
Calcule o coeficiente de atrito cinético entre o corpo $2$ e a mesa.

Sejam dois fluidos distintos cujas densidades são $1,00\ g/cm^3$ e $0,80\ g/cm^3$, colocados em um tubo vertical, como mostrado na figura. O tubo está aberto à atmosfera. Sejam $H_1 = 2,0\ m$ e $H_2 = 8,0\ m$.

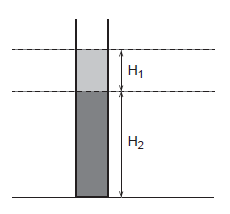
Encontre a pressão absoluta, em $kPa$, dentro do tubo, a uma altura de $4,0\ m$ em relação ao fundo do tubo.

Dados

$g = 10 \ m/s^2$

$p_{atm} = 101\ kPa$

Três blocos metálicos de mesma massa possuem calores específicos $c_1, c_2$ e $c_3$, e suas temperaturas iniciais são $T_1 = 0\ ^\circ C$, $T_2 = 30\ ^\circ C$ e $T_3 = 20\ ^\circ C$, respectivamente. Inicialmente colocam-se os blocos $1$ e $2$ em um calorímetro perfeito (com capacidade térmica desprezível) até que o equilíbrio térmico seja estabelecido, o que ocorre na temperatura de $10\ ^\circ C$. O bloco $1$ é, então, retirado do calorímetro e substituído pelo bloco $3$. A temperatura final de equilíbrio entre os blocos $2$ e $3$ é de $15\ ^\circ C$.

Calcule $c_3$, em $cal/(g.^\circ C).$

Dado

$c_1 = 0,20\ cal/(g.^\circ C)$

Considere as três afirmativas abaixo, em relação a um gás ideal.

I - Em uma compressão adiabática, a temperatura final do gás não pode ser maior do que a inicial, pois nenhum calor é trocado com a vizinhança.

II - Em um processo isocórico (isovolumétrico), nenhum trabalho é realizado pelo gás.

III - Em um processo isobárico, o trabalho realizado pelo gás é proporcional ao quadrado da variação do volume.

Marque a única opção CORRETA:

Dois trens A e B viajam em trilhos paralelos, em sentidos opostos, aproximando-se um do outro. A velocidade de ambos os trens, em módulo e em relação ao solo, é de $100\ km/h$. Quando os trens estão a uma distância de $10\ km$ um do outro, o trem $B$ começa a frear, diminuindo sua velocidade a uma taxa constante.

Sabendo-se que os trens se cruzam no exato instante em que o trem $B$ para, quanto tempo, em minutos, o trem $B$ leva em seu processo de desaceleração?