ITA 2020 Física - Questões
Abrir Opções Avançadas
Considere uma teoria na qual a força de interação entre duas “cargas generalizadas” $q_1$ e $q_2$ em universos N-dimensionais é expressa por $F_e = \dfrac{q_1q_2}{kr^{N–1}}$, em que $k$ é uma constante característica do meio. A teoria também prevê uma força entre dois “polos generalizados” $p_1$ e $p_2$ expressa por $F_m =\dfrac{ p_1p_2}{μr^{N–1}}$, na qual $μ$ é outra constante característica do meio. Sabe-se ainda que um polo $p$ pode interagir com uma corrente de carga, $i$, gerando uma força $F = \dfrac{ip}{r^{N–2}}$. Em todos os casos, $r$ representa a distância entre os entes interagentes. Considerando as grandezas fundamentais massa, comprimento, tempo e corrente de carga, assinale a alternativa que corresponde à fórmula dimensional de $kμ$.
Na figura, o anel de raio $R$ gira com velocidade angular $ω$ constante e dispõe de um alvo pontual $A$ que cruza o eixo $x $ no mesmo instante em que, do centro do anel, é disparado em sua direção um projétil puntiforme com velocidade $\vec{v_0}$. Desconsiderando a resistência do ar,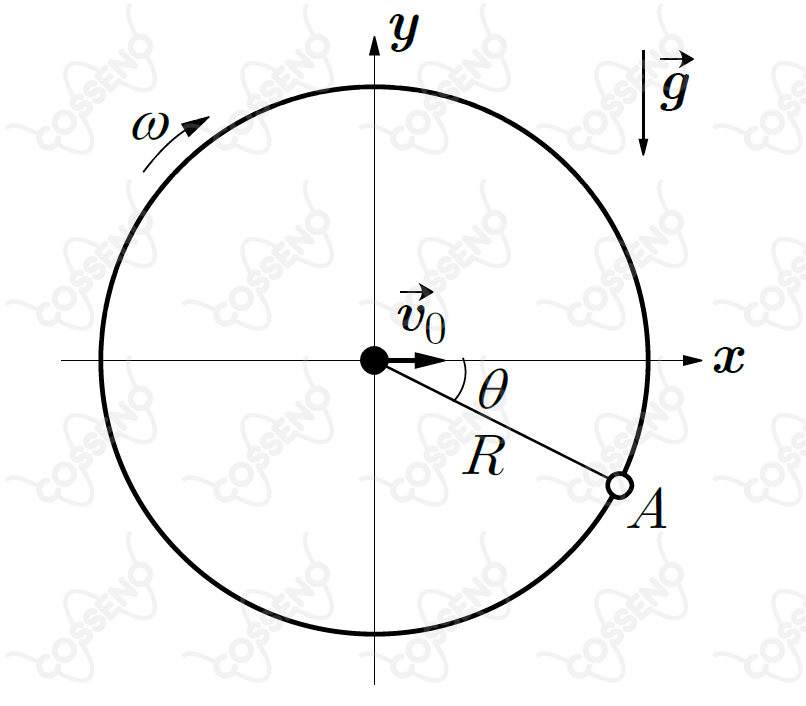
a) determine o ângulo $θ$, em relação ao eixo $x$, em que o projétil acerta o alvo;
b) determine o intervalo de tempo $∆t$ dispendido pelo projétil para acertar o alvo;
c) a velocidade angular $ω$ é determinada apenas por $θ $ e $∆t$? Justifique.
Um sistema de defesa aérea testa separadamente dois mísseis contra alvos móveis que se deslocam com velocidade $\vec{v_a}$ constante ao longo de uma reta distante de $d$ do ponto de lançamento dos mísseis. Para atingir o alvo, o míssil 1 executa uma trajetória retilínea, enquanto o míssil 2, uma trajetória com velocidade sempre orientada para o alvo. A figura ilustra o instante de disparo de cada míssil, com o alvo passando pela origem do sistema de coordenadas $xy$.
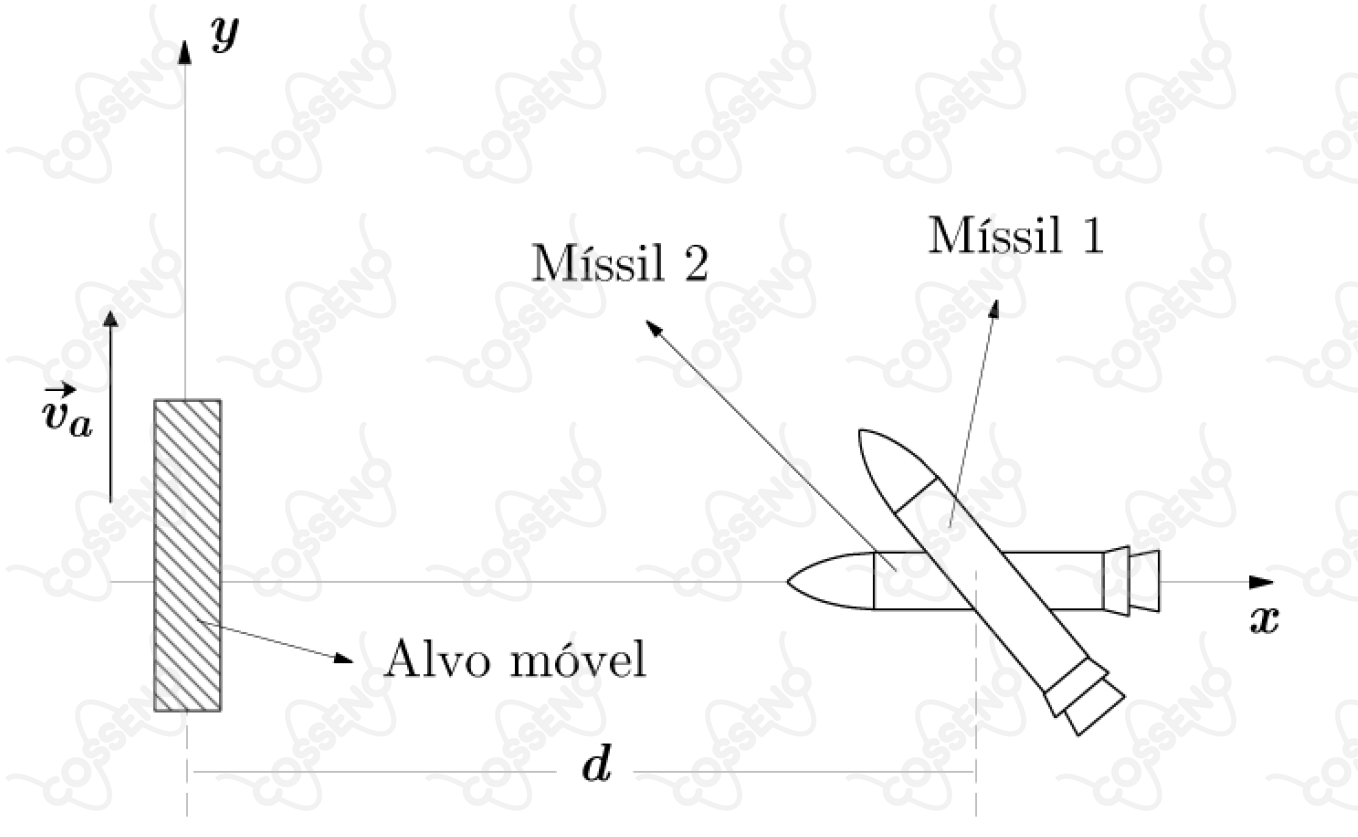
Sendo os módulos das velocidades dos mísseis iguais entre si, maiores que $v_a$ e mantidos constantes, considere as seguintes afirmações:
I. Os intervalos de tempo entre o disparo e a colisão podem ser iguais para ambos os mísseis.
II. Para que o míssil 1 acerte o alvo é necessário que o módulo da componente y de sua velocidade seja igual a $v_a$.
III. Desde o disparo até a colisão, o míssil 2 executa uma trajetória curva de concavidade positiva com relação ao sistema $xy$.
Considerando V como verdadeira e F como falsa, as afirmações I, II e III são, respectivamente,
Uma prancha retangular de espessura uniforme, $5,0\ m$ de comprimento, $1,5\ g/cm^3$ de densidade e $10\ kg$ de massa homogeneamente distribuída, é parcialmente submersa na piscina ilustrada na figura, em cuja parede (lisa) se apoia, formando um ângulo de $30^\circ$ com o piso horizontal, cujo coeficiente de atrito com a prancha é $0,6\sqrt3$.
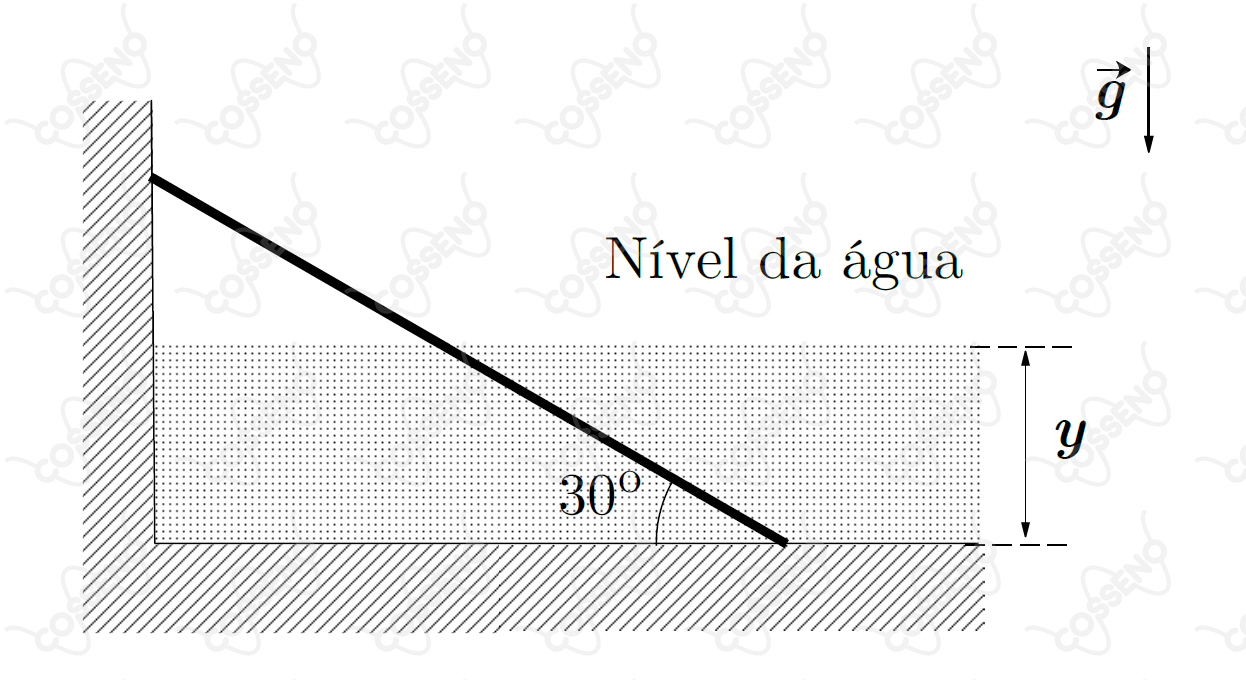
Determine para quais alturas $y$ do nível de água a prancha permanece em equilíbrio estático nessa posição.
Um bloco de massa $m$ sustentado por um par de molas idênticas, paralelas e de constante elástica $k$, desce verticalmente com velocidade constante e de módulo $v$ controlada por um motor, conforme ilustra a figura.
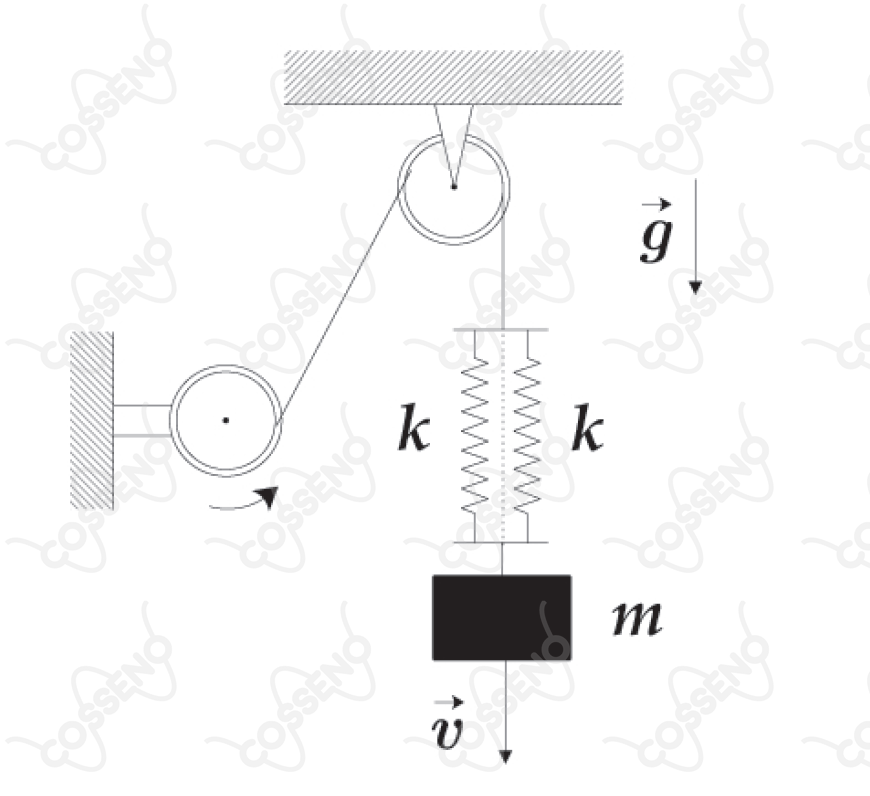
Se o motor travar repentinamente, ocorrerá uma força de tração máxima no cabo com módulo igual a
Carregando...