IME 2021 Física - Questões
Abrir Opções Avançadas
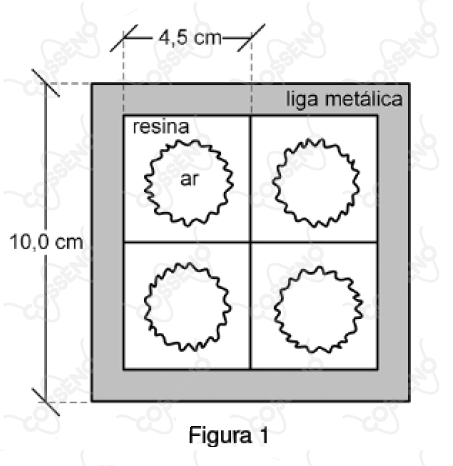
Durante a fabricação de cubos de resina com arestas de $4{,}5 \ cm$, formaram-se cavidades com $50{,}0 \ cm^{3}$ de ar no interior de cada um deles. Um artesão agrupa oito cubos, gerando um cubo maior. Em seguida, envolve essa peça com uma camada de liga metálica, formando um cubo metálico com arestas de $10{,}0 \ cm$, conforme mostra o corte da Figura $1$.
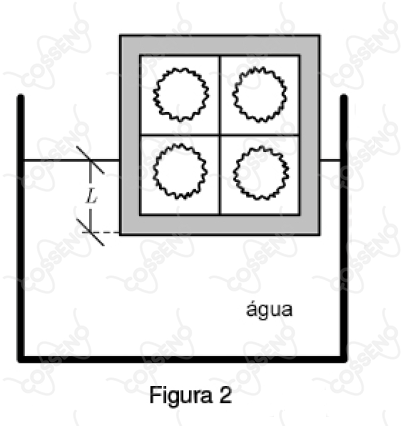
Se esse cubo metálico for colocado na água e estiver em equilíbrio, conforme mostra a Figura $2$, o valor do comprimento $L$, em $cm$, que este ficará submerso será, aproximadamente:
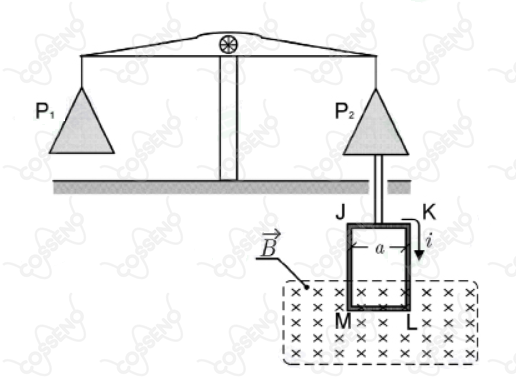
Há diversos meios de se medir a intensidade de um campo magnético. Usando-se uma balança de dois braços, com pratos $P_1$ e $P_2$, é possível fazer essa medição. A figura mostra um retângulo $\text{JKLM}$ suspenso por um dos pratos de uma balança, o qual é constituído de um número $n$ de espiras superpostas. Cada uma das espiras é percorrida por uma corrente $i$, cujo sentido inicial é mostrado na figura. A parte inferior das espiras está inserida numa região de campo magnético $\vec{B}$. Se o sentido da corrente for invertido, verifica-se a necessidade de colocar uma carga extra, de massa $m$, no prato da balança em que as espiras estão suspensas, para restaurar o equilíbrio do sistema. Considerando $g$ a aceleração da gravidade local, determine a intensidade de $\vec{B}$
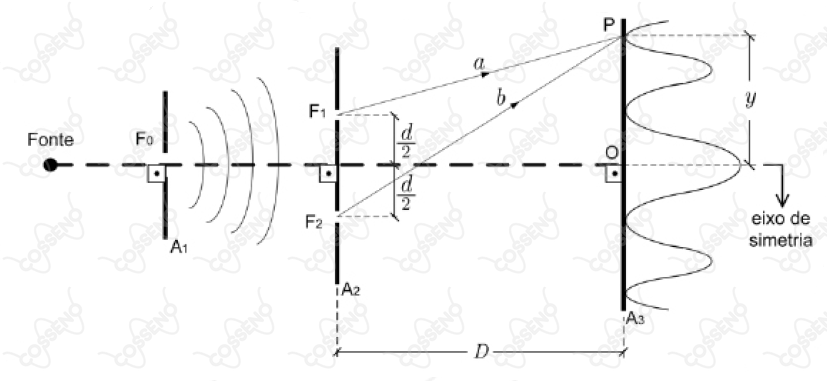
Na experiência de Thomas Young, também conhecida como experiência da fenda dupla, uma luz é difratada por uma fenda $F_0$ no anteparo $A_1$. Em seguida, o feixe de ondas difratado é novamente difratado por outras duas fendas, $F_1$ e $F_2$ no anteparo $A_2$, formando no anteparo $A_3$ um padrão de interferência constituído por franjas claras (interferência construtiva), alternadas por franjas escuras (interferência destrutiva), conforme mostra a figura.
A distância $y$ que separa as franjas (claras ou escuras) do ponto central $O$, vistas sobre o anteparo $A_3$, pode ser definida em função da distância $D$ entre os anteparos $A_2$ e $A_3$, e da distância $d$ entre as fendas $F_1$ e $F_2$. Essa distância é dada pela equação: $$y = \frac{n}{2d}Dv^{x}f^{z}$$em que: $n$ é o número de ordem da interferência; e $f$ é a frequência da luz que se propaga com velocidade $v$ nos percursos ópticos $a$ e $b$. Para que a equação seja dimensionalmente correta e para que os raios que partem de $F_1$ e $F_2$ atinjam o ponto $P$, os valores de $n$, $x$ e $z$ são, respectivamente:
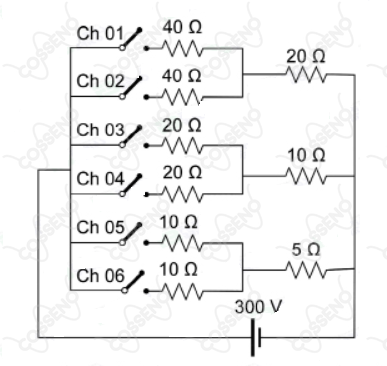
Um circuito é composto por uma fonte de tensão constante que alimenta resistores por intermédio de seis chaves. As chaves estão inicialmente abertas e mudam de estado sequencialmente nas faixas de tempo da tabela até concluir um ciclo completo:
Sequência de mudança de estados das chaves para um ciclo | ||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
Diante do exposto, pede-se:
a) a energia fornecida pela fonte, em joules, em $10$ minutos
b) a curva de potência (Watt) em função do tempo (segundo), fornecida pela fonte durante um ciclo completo
c) uma alternativa de configuração do circuito que, com chaves permanentemente fechadas, implica em um consumo de energia desde $t=0$ até $t=10$ min igual ao consumo obtido no item a)
instantaneamente
no ínicio de cada faixa de tempo - todas as chaves são abertas instantaneamente no final da faixa de tempo $10$
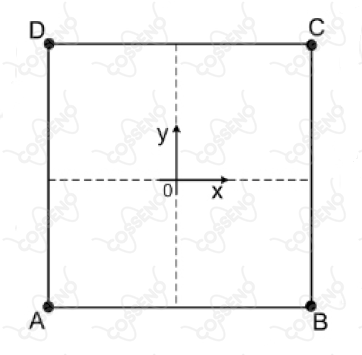
Quatro partículas, denominadas $A$, $B$, $C$ e $D$, partem simultaneamente dos vértices de um quadrado de lado unitário. Todas as partículas apresentam velocidades escalares iguais durante suas trajetórias. A partícula $A$ persegue a partícula $B$, de tal forma que o seu vetor velocidade está sempre na direção e sentido de $A$ para $B$. O mesmo ocorre entre as partículas $B$ e $C$, $C$ e $D$ e, finalmente, entre $D$ e $A$. Tomando o centro do quadrado como origem do sistema de coordenadas, a tangente do ângulo entre vetor unitário do sentido positivo do eixo $x$ e o vetor que une o ponto $A$ ao ponto $B$, quando $A$ se encontra em um ponto arbitrário $(x, y)$ da sua trajetória, é dada por:
Carregando...