IME 2019 Física - Questões
Abrir Opções Avançadas
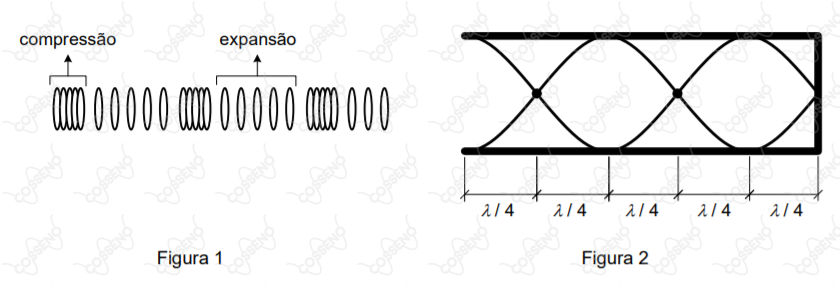
Considerando as Figuras $1$ e $2$ acima e, com relação às ondas sonoras em tubos, avalie as afirmações a seguir:
Afirmação I. as ondas sonoras são ondas mecânicas, longitudinais, que necessitam de um meio material para se propagarem, como representado na Figura $1$.
Afirmação II. uma onda sonora propagando-se em um tubo sonoro movimenta as partículas do ar no seu interior na direção transversal, como representado na Figura $2$.
Afirmação III. os tubos sonoros com uma extremidade fechada, como representado na Figura $2$, podem estabelecer todos os harmônicos da frequência fundamental.
É correto o que se afirma em:
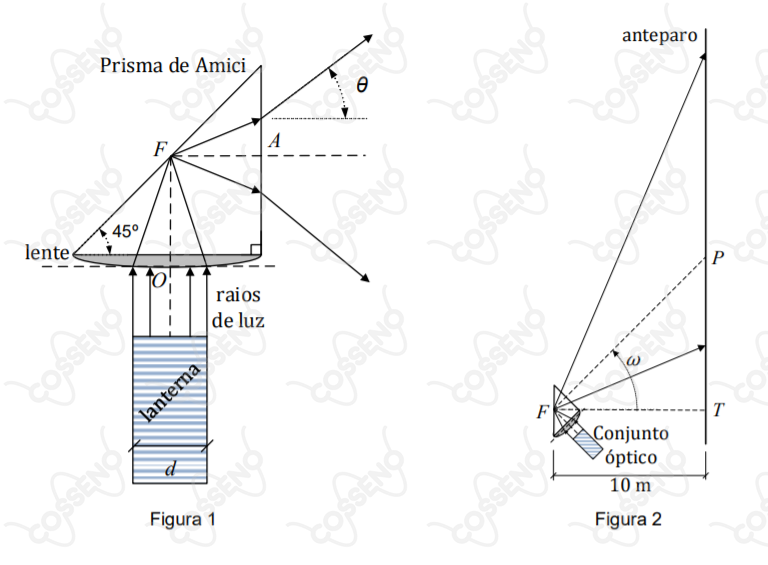
Um conjunto óptico é formado por uma lente convergente e um prisma de Amici, conforme mostra a Figura $1$. O conjunto está totalmente integrado, sendo formado pelo mesmo vidro. A lente possui centro óptico $O$ e foco $F$ situado sobre a face-hipotenusa do prisma. Nesse prisma, os raios incidentes sobre a face-hipotenusa sofrem reflexão interna total. Uma lanterna cilíndrica muito potente, com potência óptica de $P = \pi \sqrt{3} \ W$ e diâmetro $d = 10 \ cm$, gera raios de luz paralelos ao eixo principal da lente. A lanterna está solidária ao sistema óptico e seus raios são focalizados pela lente e refletidos pelo prisma, até a sua face-cateto plana, saindo do prisma e projetando a luz sobre um anteparo plano alinhado verticalmente. Conforme mostra a Figura $2$, no intervalo $0 \leq t < 12 \ s$, todo o conjunto óptico começa a girar, a partir do instante em que $P$ coincide com $T$, em velocidade angular constante $\omega = \pi/36 \ rad/s$. Dessa forma, o contorno da luz projetada no anteparo passa a ser uma curva plana, conhecida na matemática.
Diante do exposto, determine:
a) o ângulo de abertura $\theta$ do cone formado na saída do prisma, quando o índice de refração do conjunto óptico é o mínimo para que o feixe luminoso seja totalmente refletido na face-hipotenusa;
b) a expressão da velocidade escalar $v(t)$ com que o ponto $P$ (interseção do eixo do cone com o anteparo) desloca-se verticalmente ao longo do anteparo; e
c) a densidade de potência, em $W/m^{2}$, da luz projetada no anteparo, em $t = 9 \ s$. Neste caso, considere que todas as dimensões do prisma são muito pequenas em relação à distância para o anteparo, ou seja, o ângulo de abertura é $\theta$ ao longo de todo o cone de saída, a partir de $F$.
- o meio externo é o ar: $n_{1} = 1$;
- $\overline{OF} = \overline{FA} = 5(1 + 2 \sqrt{2}) \ cm$; e
- a separação horizontal entre o foco $F$ da lente e o anteparo$,$ no ponto $T,$ é $\overline{FT} = 10 \ m$.
Observação:
- a linha $\overline{FP},$ prolongamento de $\overline{FA},$ é o eixo do cone;
- o ângulo $\theta$ é o ângulo entre o eixo e qualquer geratriz do cone de luz de saída do prisma; e
- desconsidere qualquer perda da intensidade luminosa ao longo de todo o percurso até o anteparo.

Uma lanterna cilíndrica muito potente possui uma lente divergente em sua extremidade. Ela projeta uma luz sobre um anteparo vertical. O eixo central da lanterna e o eixo principal da lente estão alinhados e formam um ângulo de $45^{\circ}$ com a horizontal. A lâmpada da lanterna gera raios de luz paralelos, que encontram a lente divergente, formando um feixe cônico de luz na sua saída. O centro óptico da lente $O$ está, aproximadamente, alinhado com as bordas frontais da lanterna. A distância horizontal entre o foco $F$ da lente e o anteparo é de $1 \ m$.
Sabendo disto, pode-se observar que o contorno da luz projetada pela lanterna no anteparo forma uma seção plana cônica. Diante do exposto, o comprimento do semieixo maior do contorno dessa seção, em metros, é:
- a face côncava está na parte mais externa da lanterna
- diâmetro da lanterna: $d = 10 \ cm$
- índice de refração do meio externo (ar): $1$
- índice de refração da lente: $1{,}5$
- raio de curvatura da face côncava: $2{,}5 \ \sqrt{3} \ cm$.

A Figura $1$ ilustra um tanque industrial contendo duas entradas e uma saída, além de um circuito de aquecimento. A temperatura do líquido no interior do tanque deve ser controlada, a fim de alimentar o processo industrial conectado na saída do tanque. O agitador mistura continuamente os líquidos que chegam pelas entradas, de maneira que o volume total de líquido dentro do tanque esteja sempre numa única temperatura. A perda térmica do tanque pode ser desprezada.
Considere o tanque inicialmente vazio, com a válvula de saída fechada e o sistema de aquecimento desligado. Em $t = 0$ a válvula da entrada $1$ é aberta com uma vazão de água de $1\text{ L/min}$ à temperatura de $10^{\circ}\text{C}$ e a válvula da entrada $2$ com uma vazão de água de $0{,}25\text{ L/min}$ à temperatura de $30^{\circ}\text{C}$. Nessas condições, determine:
a) a temperatura da água no interior do tanque em $t = 50 \ min$;
b) a temperatura da água no interior do tanque em $t = 150 \ min$, se o circuito de aquecimento é ligado em $t = 50 \ min$ e a potência dissipada na resistência $R_2$, $P_{R_{2}}$,varia de acordo com o gráfico da Figura $2$; e
c) a tensão $V_F$ que deverá ser ajustada na fonte para manter a temperatura da água na saída em $22 \ ^{\circ}\text{C}$ após um longo tempo de funcionamento do sistema $(t\gg 150 \ min)$, sabendo que a válvula da entrada $2$ foi fechada, o volume no interior do tanque encontra-se nessa mesma temperatura de $22 \ ^{\circ}C$ e a válvula de saída foi aberta com a mesma vazão da válvula da entrada $1$.
- $R_{2} = 10 \ \Omega$;
- $1 \ cal = 4{,}2 \ J$;
- calor específico da água $(c) = 1 \ cal/g \cdot ^{\circ}\text{C}$; e
- densidade da água $= 1 \ kg/L$.
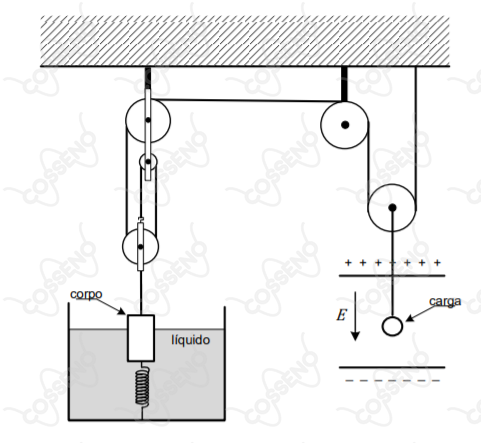
Um corpo encontra-se com $2/3$ de seu volume submerso. Uma de suas extremidades está presa por uma corda a um conjunto de roldanas que suspende uma carga puntiforme submetida a um campo elétrico uniforme. A outra extremidade está presa a uma mola distendida que está fixa no fundo do recipiente. Este sistema se encontra em equilíbrio e sua configuração é mostrada na figura acima.
Desprezando os efeitos de borda no campo elétrico, a deformação da mola na condição de equilíbrio é:
- aceleração da gravidade: $g$;
- massa específica do fluido: $\rho$;
- massa específica do corpo: $2 \rho$;
- constante elástica da mola: $k$;
- volume do corpo: $V$;
- intensidade do campo elétrico uniforme: $E$;
- massa da carga elétrica: $m$; e - carga elétrica: $+ q$.
Carregando...