IME 2018 Física - Questões
Abrir Opções Avançadas
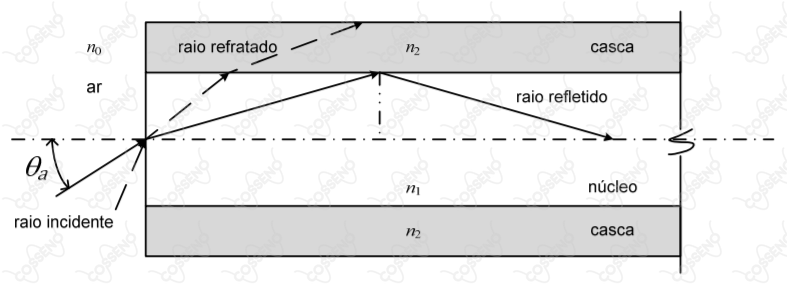
As fibras ópticas funcionam pelo Princípio da Reflexão Total, que ocorre quando os raios de luz que seguem determinados percursos dentro da fibra são totalmente refletidos na interface núcleo-casca, permanecendo no interior do núcleo. Considerando apenas a incidência de raios meridionais e que os raios retratados para a casca são perdidos, e ainda, sabendo que os índices de refração do ar, do núcleo e da casca são dados, respectivamente, por $n_0$, $n_1$ e $n_2$ ($n_1>n_2>n_0$), o ângulo máximo de incidência $\theta_a$ na interface ar-núcleo, para o qual ocorre a reflexão total no interior da fibra é:
- raios meridionais são aqueles que passam pelo centro do núcleo; e
- todas as opções abaixo correspondem a números reais.
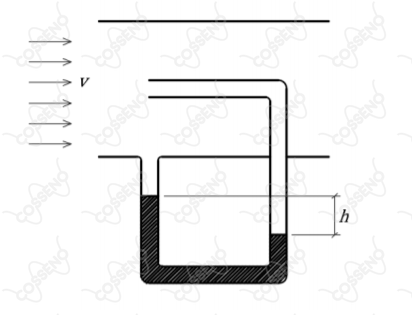
A figura acima mostra esquematicamente um tipo de experimento realizado em um túnel de vento com um tubo de Pitot, utilizado para medir a velocidade $v$ do ar que escoa no túnel de vento. Para isso, a diferença de nível $h$ entre as colunas do líquido é registrada. Em um dia frio, o experimento foi realizado e foi obtido o valor de $10,00\ cm$ para a diferença de nível $h$. Em um dia quente, o experimento foi repetido e foi obtido o valor de $10,05\ cm$ para a diferença de nível $h$. Determine:
a) o valor do coeficiente de dilatação volumétrica do líquido no interior do tubo, sabendo que a variação de temperatura entre o dia quente e o dia frio foi de $25\ K$;
b) a velocidade do ar $v$.
• a massa específica do líquido é $1.000$ vezes maior que a massa específica do ar no dia frio; e
• aceleração da gravidade: $g = 10\ m/s^2$
Considerações:
• a velocidade do ar no túnel de vento foi a mesma nos dois experimentos;
• a massa específica do ar foi a mesma nos dois experimentos;
• a aceleração da gravidade foi a mesma nos dois experimentos; e
• despreze a dilatação térmica da estrutura do tubo de Pitot.
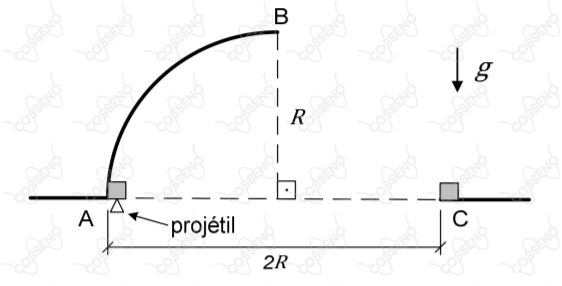
Conforme a figura acima, um corpo, cuja velocidade é nula no ponto $A$ da superfície circular de raio $R$, é atingido por um projétil, que se move verticalmente para cima, e fica alojado no corpo. Ambos passam a deslizar sem atrito na superfície circular, perdendo o contato com a superfície no ponto $B$. A seguir, passam a descrever uma trajetória no ar até atingirem o ponto $C$, indicado na figura. Diante do exposto, a velocidade do projétil é:
• massa do projétil: $m$;
• massa do corpo: $9m$; e
• aceleração da gravidade: $g$.
Uma partícula carregada tem sua posição no sistema de eixos $XY$ regida pelas seguintes equações temporais, que expressam, em metros, as coordenadas $X$ e $Y$ da partícula em função do tempo $t$:$$X(t)=\sqrt{1+\cos^2(t)-\sin^2(t)}$$ $$Y(t)=\sqrt{2+2\sin^2(t)}$$Determine:
a) a equação de uma curva que contenha a trajetória da partícula;
b) o comprimento da curva formada por todos os pontos por onde a partícula passa;
c) o tempo mínimo gasto pela partícula para trafegar por todos os pontos da curva do item anterior;
d) as coordenadas de dois pontos nos quais a velocidade da partícula é nula;
e) o gráfico do módulo da força elétrica sofrida por uma segunda partícula de mesma carga, fixada na origem, em função do tempo;
f) o gráfico da função $Q$ do vetor força magnética $F_m$ à qual estaria submetida a partícula, caso houvesse um campo magnético positivo e paralelo ao eixo $Z$, ortogonal ao plano $XY$, onde:$$Q(F_m)=\begin{cases} 1,\ \text{se }0 \leq\ \text{fase de } F_m<\frac{\pi}{2} \\ 2,\ \text{se }\frac{\pi}{2} \leq\ \text{fase de } F_m<\pi \\ 3,\ \text{se }\pi \leq\ \text{fase de } F_m<\frac{3\pi}{2} \\ 4,\ \text{se }\frac{3\pi}{2} \leq\ \text{fase de } F_m< 2\pi \end{cases}$$
• carga da partícula: $+ 4 \times 10^{-4} C$; e
• constante de Coulomb: $9 \times 10^9 \frac{Nm^2}{C^2}$.
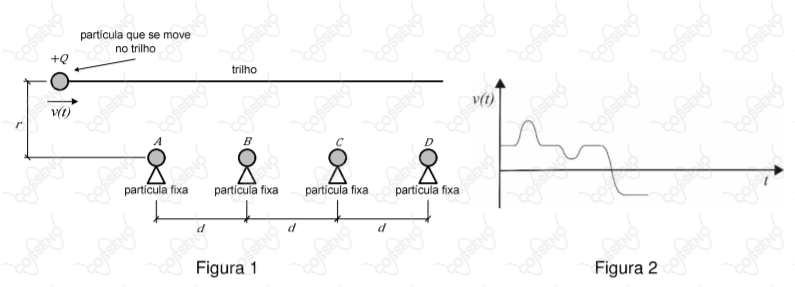
Como mostra a Figura $1$, uma partícula de carga positiva se move em um trilho sem atrito e sofre a interação de forças elétricas provocadas por outras partículas carregadas fixadas nos pontos $A$, $B$, $C$ e $D$. Sabendo que as cargas das partículas situadas em $B$ e $D$ são iguais e que uma parte do gráfico da velocidade da partícula sobre o trilho, em função do tempo, está esboçada na Figura $2$, o gráfico completo que expressa a velocidade da partícula está esboçado na alternativa:
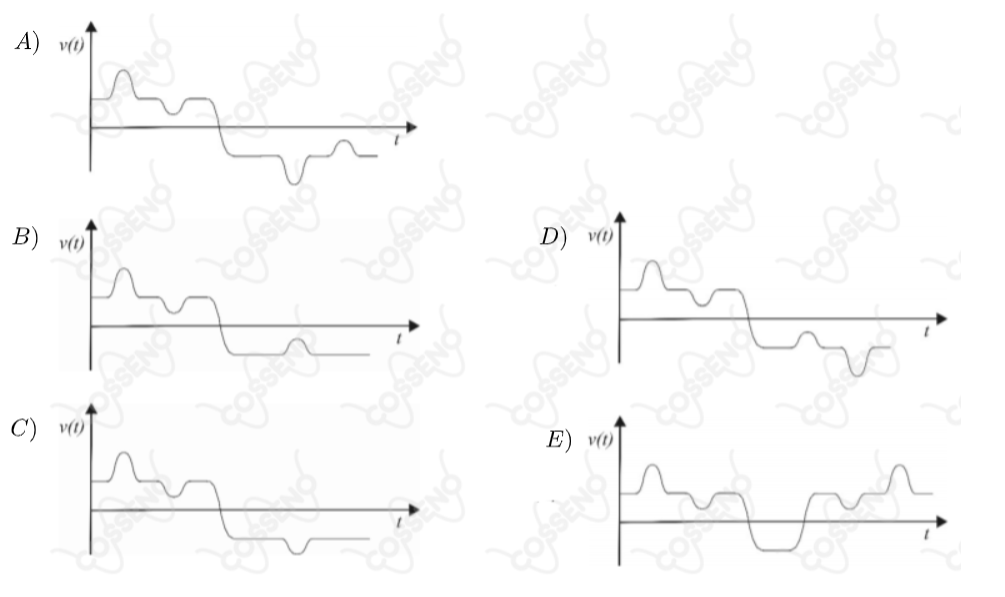
• $r<< d$;
• em $t = 0$
a partícula que se move no trilho está à esquerda da partícula situada no ponto $A$;
• considera-se positiva a velocidade da partícula quando ela se move no trilho da esquerda para a direita.
Carregando...