IME 2006 Física - Questões
Abrir Opções Avançadas
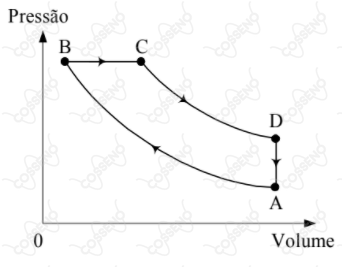
O ciclo Diesel, representado na figura abaixo, corresponde ao que ocorre num motor Diesel de quatro tempos: o trecho $AB$ representa a compressão adiabática da mistura de ar e vapor de óleo Diesel; $BC$ representa o aquecimento a pressão constante, permitindo que o combustível injetado se inflame sem necessidade de uma centelha de ignição; $CD$ é a expansão adiabática dos gases aquecidos movendo o pistão e $DA$ simboliza a queda de pressão associada à exaustão dos gases da combustão. A mistura é tratada como um gás ideal de coeficiente adiabático $\gamma$. Considerando que $T_A$, $T_B$, $T_C$ e $T_D$ representam as temperaturas, respectivamente, nos pontos $A$, $B$, $C$ e $D$, mostre que o rendimento do ciclo Diesel é dado por:
$$\eta = 1-\frac{1}{\gamma}\left( \frac{T_D-T_A}{T_C-T_B}\right)$$
Um corpo de $500\ g$ de massa está inicialmente ligado a uma mola. O seu movimento é registrado pelo gráfico abaixo, que mostra a aceleração em função da posição, a partir do ponto em que a mola se encontra com a compressão máxima. A abscissa $x = 0$ corresponde à posição em que a deformação da mola é nula. Nesta posição, o corpo foi completamente liberado da mola e ficou submetido à aceleração registrada no gráfico. Determine:

a) a variação da quantidade de movimento nos $2\ s$ após o corpo ser liberado da mola;
b) o trabalho total realizado desde o começo do registro em $x = -0,5\ m$ até $x = 3\ m$.
Um raio luminoso incide ortogonalmente no ponto central de um espelho plano quadrado $MNPQ$, conforme a figura abaixo. Girando-se o espelho de um certo ângulo em torno da aresta $PQ$, consegue-se que o raio refletido atinja a superfície horizontal $S$ paralela ao raio incidente. Com a sequência do giro, o ponto de chegada em $S$ aproxima-se da aresta $PQ$. No ponto de chegada em $S$ que fica mais próximo de $PQ$ está um sensor que, ao ser atingido pelo raio refletido, gera uma tensão elétrica $U$ proporcional à distância $d$ entre o referido ponto e aquela aresta: $U = k.d$. Fixando o espelho na posição em que a distância $d$ é mínima, aplica-se a tensão $U$ aos terminais $A$ e $B$ do circuito.
Dado que todos os capacitores estão inicialmente descarregados, determine a energia que ficará armazenada no capacitor $C_3$ se a chave $Y$ for fechada e assim permanecer por um tempo muito longo.
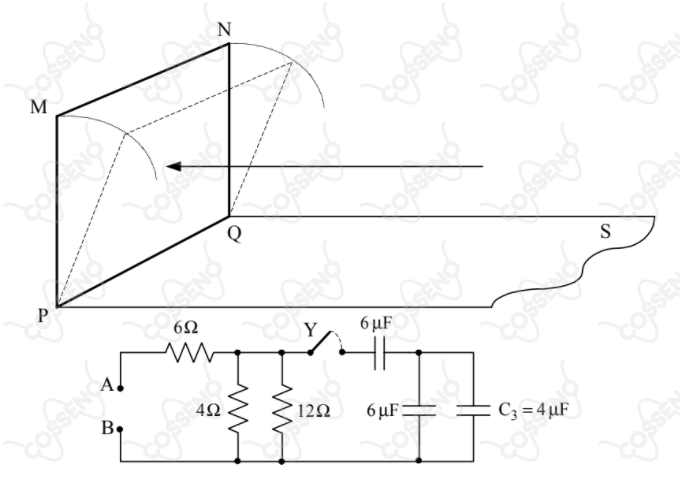
constante $k = 12\ V / m$.
Para ferver dois litros de água para o chimarrão, um gaúcho mantém uma panela de $500\ g$ suspensa sobre a fogueira, presa em um galho de árvore por um fio de aço com $2\ m$ de comprimento. Durante o processo de aquecimento são gerados pulsos de $100\text{ Hz}$ em uma das extremidades do fio. Este processo é interrompido com a observação de um regime estacionário de terceiro harmônico. Determine:
a) o volume de água restante na panela;
b) a quantidade de energia consumida neste processo.
aceleração da gravidade $(g)= 10\ m/s^2$;
massa específica da água $= 1\ kg / \ell$;
calor latente de vaporização da água $= 2,26\ MJ/ kg$.
Uma partícula parte do repouso no ponto $A$ e percorre toda a extensão da rampa $ABC$, mostrada na figura abaixo. A equação que descreve a rampa entre os pontos $A$, de coordenadas $(0,h)$ e $B$, de coordenadas $(h,0)$, é
$$y=\dfrac{x^2}{h}-2x+h$$
enquanto entre os pontos $B$ e $C$, de coordenadas $(h,2r)$, a rampa é descrita por uma circunferência de raio $r$ com centro no ponto de coordenadas $(h,r)$. Sabe-se que a altura $h$ é a mínima necessária para que a partícula abandone a rampa no ponto $C$ e venha a colidir com ela em um ponto entre $A$ e $B$. Determine o ponto de colisão da partícula com a rampa no sistema de coordenadas da figura como função apenas do comprimento $r$.

Carregando...