IME 2005 - Questões

Sejam $a, b, c$ e $d$ números reais positivos e diferentes de $1$. Sabendo que $\log_a d, \log_b d$ e $\log_c d$ são termos consecutivos de uma progressão aritmética, demonstre que:$$c^2=(ac)^{\log_a d}$$

Resolva a equação

$$2 \sin11x + \cos 3x + \sqrt3 \sin 3x = 0$$

Considere uma elipse de focos $F$ e $F^\prime$ , e $M$ um ponto qualquer dessa curva. Traça-se por $M$ duas secantes $\overline{MF}$ e $\overline{MF^\prime}$, que interceptam a elipse em $P$ e $P^\prime$, respectivamente. Demonstre que a soma $(\overline{MF}/\overline{FP}) + ( \overline{MF^\prime}/\overline{F^\prime P^\prime})$ é constante.

Sugestão: calcule inicialmente a soma $(1/\overline{MF} ) + (1/\overline{FP})$.

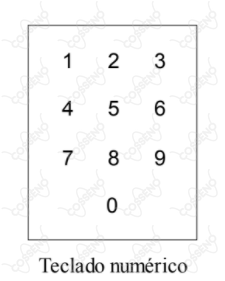
O sistema de segurança de uma casa utiliza um teclado numérico, conforme ilustrado na figura. Um ladrão observa de longe e percebe que:

• a senha utilizada possui $4$ dígitos;

• o primeiro e o último dígitos encontram-se numa mesma linha;

• o segundo e o terceiro dígitos encontram-se na linha imediatamente superior.

Calcule o número de senhas que deverão ser experimentadas pelo ladrão para que com certeza ele consiga entrar na casa.

Calcule o determinante da matriz $n \times n$ em função de $b$, onde $b$ é um número real tal que $b^2\neq 1$.

$$\begin{vmatrix} b^2 + 1 & b & 0 & \cdots & 0 & 0 \\ b & b^2 +1 & b & \cdots & 0 & 0 \\ 0 & b& b^2+1&\cdots&0&0\\ 0&0&b&\cdots&0&0\\\vdots&\vdots&\vdots&\ddots&\vdots&\vdots\\0&0&0&\cdots&b^2+1&b\\0&0&0&\cdots &b &b^2+1 \end{vmatrix}$$