IME 2003 Física - Questões
Abrir Opções Avançadas
Um pequeno refrigerador para estocar vacinas está inicialmente desconectado da rede elétrica e o ar em seu interior encontra-se a uma temperatura de $27\ ^{\circ}C$ e pressão de $1 \ atm$. O refrigerador é ligado até atingir a temperatura adequada para refrigeração que é igual $18 \ ^{\circ}C$. Considerando o ar como gás ideal, determine a força mínima necessária, em $kgf$, para abrir a porta nesta situação, admitindo que suas dimensões sejam de $10 \ cm$ de altura por $20 \ cm$ comprimento.
Uma experiência é realizada em um recipiente termicamente isolado, onde são colocados: $176{,}25 \ ml$ de água a $293 \ K$; um cubo de uma liga metálica homogênea com $2{,}7 \ kg$ de massa, aresta de $100 \ mm$, a $212 \ ^{\circ}F$; e um cubo de gelo de massa $m$, a $-10 \ ^{\circ}C$. O equilíbrio térmico é alcançado a uma temperatura de $32 \ ^{\circ}E$, lida em um termômetro graduado em uma escala $E$ de temperatura. Admitindo que o coeficiente de dilatação linear da liga metálica seja constante no intervalo de temperaturas da experiência, determine:
a) A equação de conversão, para a escala Celsius, de uma temperatura $t_{E}$, lida na escala $E$.
b) A massa $m$ de gelo, inicialmente a $-10 \ ^{\circ}C$, necessária para que o equilíbrio ocorra a $32 \ ^{\circ}E$.
c) O valor da aresta do cubo da liga metálica a $32 \ ^{\circ}E$.
Calor específico da liga metálica: $0{,}20 \ cal/(g \cdot\, ^{\circ}C)$.
Calor específico do gelo: $0{,}55 \ cal/(g \cdot\, ^{\circ}C)$.
Calor específico da água: $1{,}00 \ cal/(g \cdot\, ^{\circ}C)$.
Calor latente de fusão da água: $80 \ cal/g$.
Massa específica da água: $1 \ g/cm^{3}$
Temperatura de fusão da água na escala $E$: $-16\ ^{\circ}E$.
Temperatura de ebulição da água na escala $E$: $+64\ ^{\circ}E$.
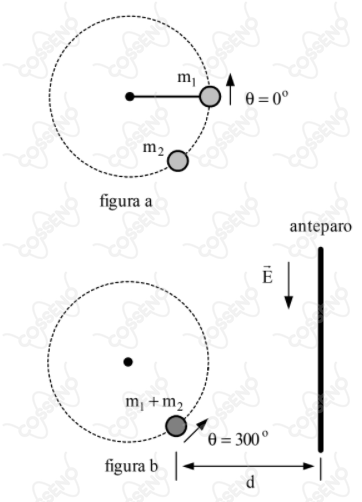
Um corpo de massa $m_1$ está preso a um fio e descreve uma trajetória circular de raio $1/ \pi \ m$. O corpo parte do repouso em $\theta = 0 ^{\circ}$ (figura $a$) e se movimenta numa superfície horizontal sem atrito, sendo submetido a uma aceleração angular $\alpha = 6 \pi /5 \ rad /s ^{2}$. Em $\theta = 300^{\circ}$ (figura $b$) ocorre uma colisão com um outro corpo de massa $m_2$ inicialmente em repouso. Durante a colisão o fio é rompido e os dois corpos saem juntos tangencialmente à trajetória circular inicial do primeiro. Quando o fio é rompido, um campo elétrico $E$ (figura $b$) é acionado e o conjunto, que possui carga total $+Q$, sofre a ação da força elétrica. Determine a distância $d$ em que deve ser colocado um anteparo para que o conjunto colida perpendicularmente com o mesmo.
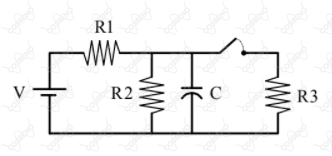
Um circuito composto por uma fonte, três resistores, um capacitor e uma chave começa a operar em $t = - \infty$ com o capacitor inicialmente descarregado e a chave aberta. No instante $t = 0$, a chave é fechada. Esboce o gráfico da diferença de potencial nos terminais do capacitor em função do tempo, indicando os valores da diferença de potencial para $t = - \infty$, $t = 0$ e $t = + \infty$.
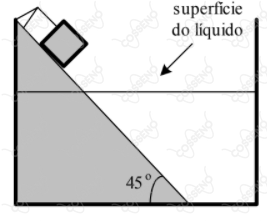
Um pequeno bloco pesando $50 \ N$ está preso por uma corda em um plano inclinado, como mostra a figura. No instante $t = 0 \ s$, a corda se rompe. Em $t = 1 \ s$, o bloco atinge o líquido e submerge instantaneamente. Sabendo que o empuxo sobre o bloco é de $50 \ N$, e que o coeficiente de atrito dinâmico entre o bloco e a parte emersa do plano inclinado é $0{,}4$ , determine a distância percorrida pelo bloco a partir do instante inicial até $t = 3 \ s$.
Carregando...