IME 2002 - Questões
Abrir Opções Avançadas
Considere uma parábola de eixo focal $Ox$ que passe pelo ponto $(0{,} \ 0)$. Define-se a subnormal em um ponto $P$ da parábola como o segmento de reta ortogonal à tangente da curva, limitado pelo ponto $P$ e o eixo focal. Determine a equação e identifique o lugar geométrico dos pontos médios das subnormais dessa parábola.
a) Encontre as condições a que devem satisfazer os coeficientes de um polinômio $P(x)$ de quarto grau para que $P(x) = P(1 - x)$.
b) Considere o polinômio $P(x) = 16x^4 - 32x^3 - 56x^2 + 72x+ 77$. Determine todas as suas raízes sabendo-se que o mesmo satisfaz a condição do item acima.
Quatro cidades, $A$, $B$, $C$ e $D$, são conectadas por estradas conforme a figura abaixo. Quantos percursos diferentes começam e terminam na cidade $A$, e possuem:
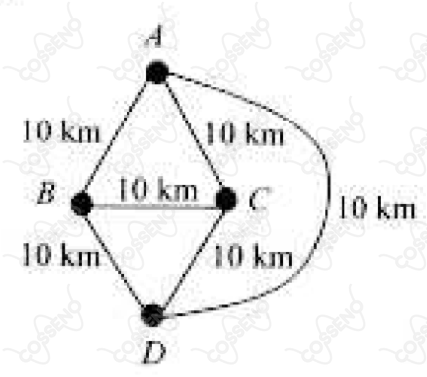
a) Exatamente $50 \ km$?
b) $n \times 10 \ km$?
Uma matriz quadrada é denominada ortogonal quando a sua transposta é igual a sua inversa. Considerando esta definição, determine se a matriz $[R]$, abaixo, é uma matriz ortogonal, sabendo-se que $n$ é um número inteiro e $\alpha$ é um ângulo qualquer. Justifique a sua resposta.
$\begin{bmatrix} R \end{bmatrix} = \begin{bmatrix} \cos{(n \alpha)} & -\sin{(n \alpha)} & 0 \\ \sin{(n \alpha)} & \cos{(n \alpha)} & 0 \\ 0 & 0 & 1 \\ \end{bmatrix}$
Resolva a equação $\sqrt{5 - \sqrt{5 - x}} = x$, sabendo-se que $x > 0$.
Carregando...