IME 1956 Matemática - Questões
Abrir Opções Avançadas
Determinar os valores inteiros de x, y e z que verificam o sistema:$$\begin{cases}\log_2{y}+\log_x{z}=8\\y=x^2\\x=\frac{\sqrt[3]{z}}{2}\end{cases}$$
Os vértices de um cubo de lado $L$ são centros de esferas de raio $1/2$. No espaço interno delimitado pelas superfícies de todas as esferas, inscrevem-se dois poliedros regulares convexos $P_1$ e $P_2$. O primeiro, $P_1$, é tal que suas faces são tangentes às esferas e o segundo, $P_2$, é tal que todos os seus vértices estão, cada um em uma superfície esférica. Determinar a relação entre os volumes dos dois poliedros.
Determinar $y$ em função de $x$, de tal modo que se tenha a igualdade: $$C_y^x=C_y^{x-1}$$
Sabendo-se que nos triângulos $ABC$ e $A^\prime B^\prime C^\prime$ da figura, o lado $\overline{AC}$ é a bissetriz do ângulo ${\hat A^\prime}$ e o lado $\overline{{B^\prime}{C^\prime}}$ é a bissetriz do ângulo $\hat B$, pedem-se:
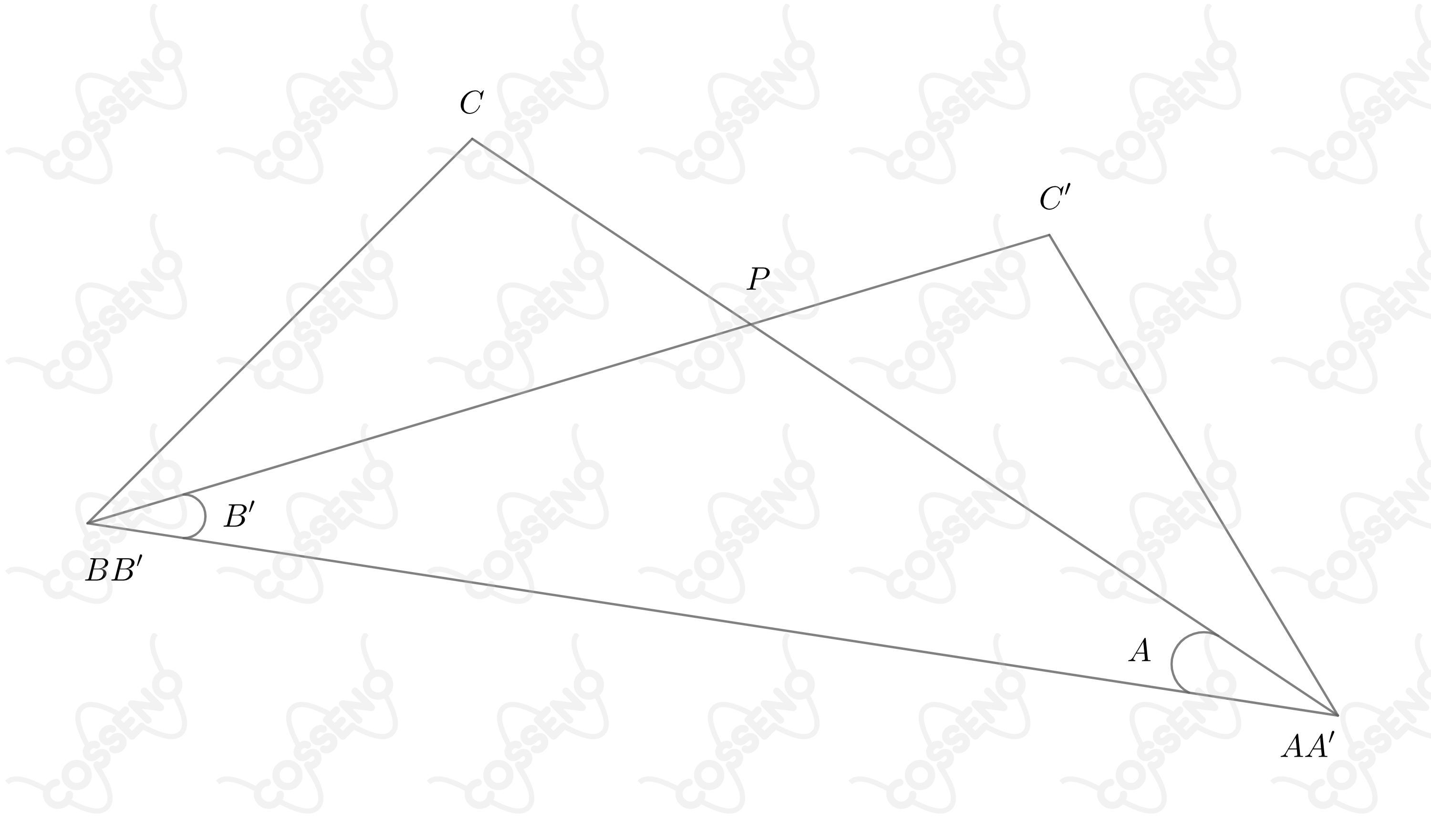
a) Determinar o valor de $\hat A^\prime + \hat B$ tendo em vista que $$\tan{(\hat A+\hat B^\prime)}+\tan{\left[ \frac{\pi}{2}+(\hat A+\hat B^\prime)\right] }+\tan{\left [\frac{\pi}{2}- 2(\hat A+\hat B^\prime)\right ]}=0$$
b) Mostrar que $$\sin{\hat A}.\sin{\hat B^\prime} =\frac{{\overline{AC}\times\overline{{B^\prime}{C^\prime}}}}{{4\overline{AB}}^2}$$
c) Mostrar que$$\cos{\hat A}.\cos{\hat B^\prime}=\frac{2m.n}{\overline{AC}\times\overline{{B^\prime}{C^\prime}}}$$ sendo $m$ e $n$ as projeções de $\overline{AP}$ e $\overline{BP}$ sobre $\overline{AB}$.
d) Mostrar que em um triângulo retângulo a área é igual ao produto dos segmentos determinados pelo círculo inscrito sobre a hipotenusa.
Achar a soma da série: $$1+\frac{1}{3}+\frac{1}{8}+\frac{1}{15}+\frac{1}{24}+...$$
Carregando...