ESPCEX 2010 Matemática - Questões
Abrir Opções Avançadas
A represa de uma usina hidroelétrica está situada em uma região em que a duração do período chuvoso é $\pu{100 \text{dias}}$. A partir dos dados hidrológicos dessa região, os projetistas concluíram que a altura do nível da represa varia, dentro do período chuvoso, segundo a função Real $$N(t) = \begin{cases} \dfrac{t}{5} + 8, & \text{para } 0\le t < 20 \\ \\ -\dfrac{t^2}{100} + \dfrac{4t}{5}, & \text{para } 20 \le t < 50 \\ \\ -\dfrac{3t}{25} + 21, & \text{para } 50 \le t < 100\end{cases}$$Em que $N(t)$ é a altura do nível da represa, medido em metros, $t$ é o número de dias, contados a partir do início do período chuvoso. Segundo esse modelo matemático, o número de dias, dentro do período chuvoso, em que a altura do nível da represa é maior ou igual a $\pu{12 \text{metros}}$ é
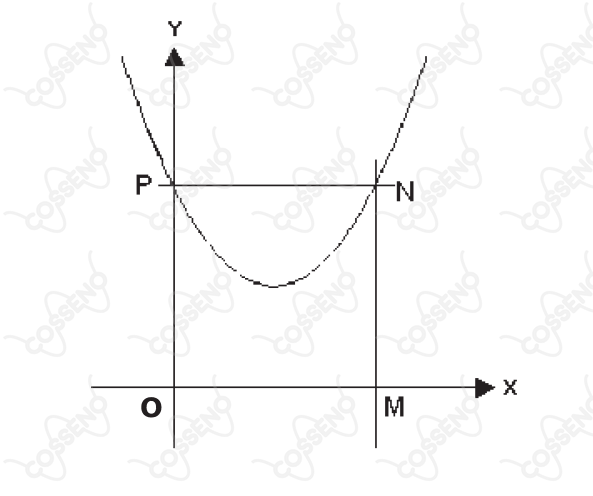
Na figura abaixo, estão representados um sistema de eixos coordenados com origem $O$, o gráfico de uma função real do tipo $f(x)=ax^2+bx+c $ e o quadrado $\mathit{OMNP}$, com $\pu{16 \text{unidades}}$ de área. Sabe-se que o gráfico de $f(x)$ passa pelos pontos $P$ e $N$, vértices do quadrado, e pelo ponto de encontro das diagonais desse quadrado. Assim, o valor de $a+b+c$ é
Dada a expressão$\left( \dfrac{1}{3}\right)^{\displaystyle 4x - x^{2}},$ em que $x$ é um número real qualquer, podemos afirmar que
Sendo $x = \sqrt[\displaystyle 6]{\dfrac{\displaystyle a^2}{\displaystyle b}}$, com $\log_{2} a = 4$ e $\log_{2} b = 5$, em que $a$ e $b$ são números reais não nulos e diferentes de $1$, então $\log_{x} 2$ é igual a
O conjunto-solução da inequação $\displaystyle x^{ \textstyle \log_x (x+1)^2} \le 4$, no conjunto dos números Reais, é
Carregando...