ESPCEX 2001 Matemática - Questões
Abrir Opções Avançadas
A equação $5^{2x +1}=15$ pode ser resolvida dispondo-se de uma tabela de logaritmos decimais. O valor de $x$ que a satisfaz é:
Numa partida de basquetebol, uma equipe, entre cestas de $2$ (dois) pontos e $3$ (três) pontos, fez $40$ cestas, totalizando $98$ pontos. Pode-se dizer que o número de cestas de $3$ (três) pontos dessa equipe foi de:
A função $f(x) = x^2 -256-10^{-16}$ tem como uma de suas raízes:
Para todo $x \in R - \begin{Bmatrix} \frac{k\pi}{2} , k \in Z \end{Bmatrix}$, simplificando a expressão $\frac{1}{1 + \sin{x}^2} + \frac{1}{1 + \csc {x}^2} + \frac{1}{1 + \cos{x}^2} + \frac{1}{1 + \sec{x}^2}$ , obtém-se o valor:
Denomina-se rolamento a um dispositivo mecânico constituído por dois anéis em forma de casca cilíndrica e um conjunto de esferas. Desejando obter o volume de uma das esferas de aço que compõe o rolamento dado na figura $1$, sem desmontá-lo, e não dispondo de todos os instrumentos necessários para executar as medições, um estudante executou os seguintes procedimentos:
a. Com os instrumentos de que dispunha, mediu o anel interno, em forma de casca cilíndrica, obtendo $\pu{3,46 cm}$ para o diâmetro interno, $\pu{4 cm}$ para o diâmetro externo e $\pu{1 cm}$ para altura;
b. Repetiu as operações para o anel externo, anotou as medidas e calculou o volume, obtendo $\pu{3,8 cm3}$ ;
c. Lembrando o princípio de Arquimedes, que afirma que o volume de um objeto imerso num recipiente com líquido corresponde à variação do volume do líquido, colocou água numa proveta graduada em $\pu{cm3}$ , conforme a figura 2, mergulhou o rolamento na água e obteve a leitura indicada na figura 3.
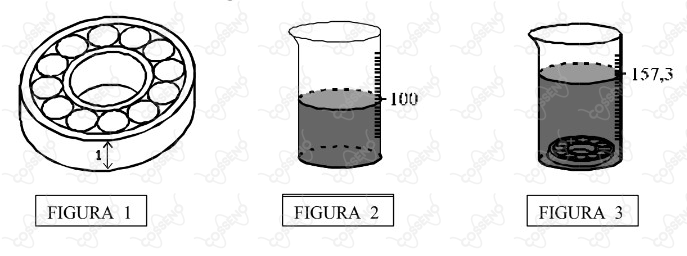
Nessas condições pode-se afirmar que o valor que mais se aproxima do volume de cada esfera, em $\pu{cm3}$ , é:
Carregando...