EPCAR 2013 Matemática - Questões
Abrir Opções Avançadas
O oposto do número real $x=\dfrac{526}{495} +\left[\dfrac{\left(\left(-2\right)^{\left(2\sqrt{2} -1\right)} \right)^{\left(2\sqrt{2} +1\right)} }{128} \right]^{-1}$ está compreendido entre
A equação $x = \sqrt{3x+a^2+3a}$ , em que x é a incógnita e $a \in \mathbb{R}$ tal que $a < -3$ , possui conjunto solução $S$, $S \subset \mathbb{R}$ Sobre $S$ tem-se as seguintes proposições:
I. Possui exatamente dois elementos.
II. Não possui elemento menor que $2$
III. Possui elemento maior que $3$
Sobre as proposições acima, são verdadeiras
“NASCIDOS PARA VOAR: 60 ANOS DE FUMAÇA JÁ”
(Fonte: Jornal EPCARIANO - Ano 1,nº 01 p. 4 )
Em maio de 2012, o esquadrão EDA (Esquadrilha da Fumaça) comemorou 60 anos de apresentações.
Para homenagear esse esquadrão foi realizado na EPCAR um concurso em que os alunos teriam que criar um desenho.
Uma das regras desse concurso foi: elaborar um desenho usando conhecimentos de matemática.
O aluno vencedor apresentou o desenho em circunferências conforme esquema abaixo.
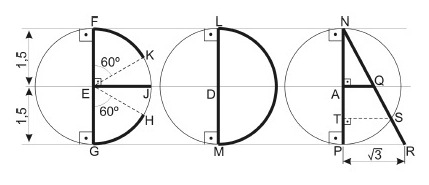
Com base nas informações do desenho, julgue verdadeira ou falsa cada afirmativa.
(02) A menor soma das medidas dos comprimentos dos arcos $\widehat{PS}$, $\widehat{GH}$,$\widehat{FK}$ e $\widehat{LM}$ é igual a $6\ \pi$
(04) A razão entre $\overline{PS}$ e $\overline{ST}$, nessa ordem, é $\frac{2\sqrt{3} }{3}$
(08) $\overline{PS}$ e $\overline{GH}$ são congruentes
(16) $\overline{AQ\ }=\frac{1}{2} \overline{EJ}$
(32) $\overline{ST\ }= \frac{3\sqrt{3} }{4}$
A soma das alternativas verdadeiras é igual a
Uma professora de Matemática do $5$º ano do Ensino Fundamental, para dar início a um conteúdo novo, levou para a sala de aula p bolinhas em uma única caixa.
Ela chamou os alunos $\alpha ,\ \beta ,\ \gamma$ à frente da turma e pediu a cada aluno que, um de cada vez, fizesse retiradas sucessivas de um mesmo número de bolinhas, conforme descrito no quadro abaixo:
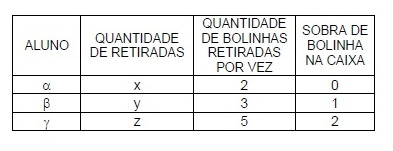
Sabe-se que:
I. $40\ <\ p\ <\ 80$
II. Cada aluno, logo após a contagem das bolinhas por ele retiradas, devolveu todas as bolinhas para a caixa.
III. Não houve erro na contagem por parte dos alunos.
Com base nessas informações, é FALSO que
Hoje, dia $29$ de julho de $2012$, José tem o dobro da idade que Luiz tinha quando José tinha a idade que Luiz tem. Quando Luiz tiver a idade que José tem, a soma das idades deles será $90$ anos.
Em $29$ de julho de $2017$, a razão entre as idades de José e Luiz, nessa ordem, será
Carregando...