EPCAR 2012 - Questões

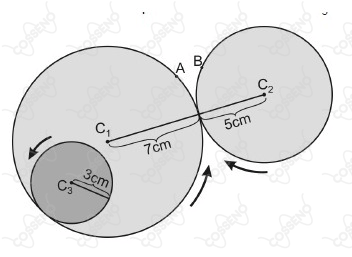
Os círculos abaixo têm centros fixos em $C_1,\ C_2,\ C_3$ e se tangenciam conforme a figura. Eles giram conforme a direção das setas, e não derrapam nos pontos de contato. Num certo momento, os pontos $A$ e $B$ das circunferências de centros $C_1$ e $C_2$ se encontram no ponto de tangência. A partir desse momento até $A$ e $B$ se encontrarem novamente, o número de voltas dadas pelo círculo de centro em $C_3$ é

Um reservatório d’água na forma de um paralelepípedo reto de base quadrada e cuja altura é metade do lado da base, está com $80\%$ de sua capacidade máxima ocupada. Se fosse preciso acabar de encher este reservatório seriam necessários $500$ baldes iguais cheios d’água com capacidade de $12800\ \text{mL}$ cada. Com base nesses dados, é correto afirmar que a altura da água que há neste reservatório

Sobre a equação $kx-\dfrac{x-1}{k} =1$, na variável $\mathbf{x}$, é correto afirmar que

De 2002 a 2010 “a carga tributária saltou de 32,7% para 37% (...) O brasileiro médio tem de trabalhar 148 dias por ano para pagar seus impostos. ”

(Fonte: Revista Veja de 05/01/2011, pag. 78)

O gráfico abaixo representa o volume de tributos (em percentual) cobrados pelo governo de 2002 a 2010.

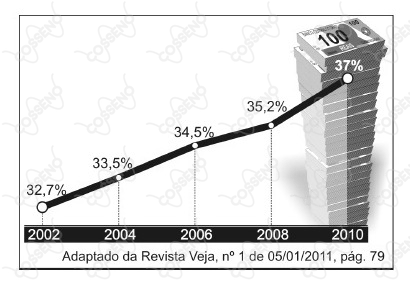
Com base nas informações do gráfico, marque a alternativa FALSA.

Considere a parábola que representa a igualdade $y=ax^2+bx+c$, de eixo de simetria $\mathop{PV}\limits^{\longleftrightarrow}$ , e o quadrado $ABCD$ indicados na figura abaixo.

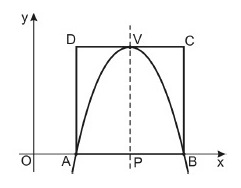
Sabendo-se que os pontos $A$ e $B$ pertencem à parábola e ao eixo $\mathop{OX}\limits^{\longleftrightarrow}$ e sendo $V$ o ponto onde a parábola tangencia o segmento $\overline{DC}$, o valor de $\Delta =b^2-4ac$ é