ENEM 2021 Matemática - Questões

O sistema de numeração Romano ainda é utilizado na indicação de capítulos e volumes de livros, na designação de séculos e, em ordem cronológica, de papas e reis de mesmo nome. São utilizadas sete letras do alfabeto:

$\bullet$ Quatro fundamentais: $I$ (vale $1$); $X$ (vale $10$); $C$ (vale $100$) e $M$ (vale $1000$).

$\bullet$ Três secundárias: $V$ (vale $5$); $L$ (vale $50$) e $D$ (vale $500$).

As regras para escrever números romanos são:

$1 -$ Não existe número correspondente ao zero;

$2 -$ Os símbolos fundamentais podem ser repetidos até três vezes e seus valores são adicionados. Exemplo:

$$XXX = 30;$$

$3 -$ Uma letra posta à esquerda de outra de maior valor indica subtração dos respectivos valores. Exemplo:

$$IX = 10 - 1 = 9;$$

$4-$ Uma letra posta à direita de outra de maior valor indica adição dos respectivos valores. Exemplo:

$$XI = 10 + 1 = 11;$$

Em uma cidade europeia há uma placa indicando o ano de sua fundação: $MCDLXIX$. Quantos anos de fundação essa cidade comemorará em $2050$?.

Uma unidade de medida comum usada para expressar áreas de terrenos de grandes dimensões é o hectares, que equivale a $10.000\ m^2$. Um fazendeiro decide fazer um loteamento utilizando $3$ hectares de sua fazenda, dos quais $0,9$ hectare será usado para construção de ruas e calçadas e o restante será dividido em terrenos com área de $300 \ m^2$ cada um. Os $20$ primeiros terrenos vendidos terão preços promocionais de R$ $20.000,00$ cada, e os demais R$ $30.000,00$ cada.

Nas condições estabelecidas, o valor total, em real, obtido pelo fazendeiro com a venda de todos os terrenos será igual a:

Uma pessoa produzirá uma fantasia utilizando como materiais: $2$ tipos de tecidos diferentes e $5$ tipos distintos de pedras ornamentais. Essa pessoa tem à sua disposição $6$ tecidos diferentes e $15$ pedras ornamentais distintas.

A quantidade de fantasias com materiais diferentes que podem ser produzidas é representada pela expressão:

Os diretores de uma escola precisam construir um laboratório para uso dos alunos. Há duas possibilidades:

$(i) -$ um laboratório do tipo $A$, com capacidade para $100$ usuários, a um custo de $180$ mil reais e gastos de $60$ mil reais por ano para manutenção;

$(ii) -$ um laboratório do tipo $B$, com capacidade para $80$ usuários, a um custo de $120$ mil reais e gastos com manutenção de $16$ mil reais por ano.

Considera-se que, em qualquer caso o laboratório implantado será utilizado na totalidade de sua capacidade.

A economia da escola, na utilização de um laboratório tipo $B$, em vez de um laboratório tipo $A$, num período de $4$ anos, por usuário, será de:

Um ciclista amador de $61$ anos de idade utilizou um monitor cardíaco para medir suas frequências cardíacas em quatro diferentes tipos de trechos do percurso. Os resultados das frequências cardíacas máximas alcançadas nesses trechos foram:

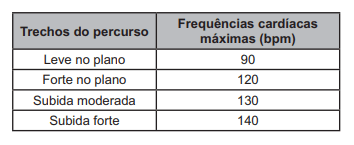
Sabe-se que a faixa aeróbica ideal para o ganho de condicionamento físico é entre $65\%$ e $85\%$ da frequência cardíaca máxima $(F_{c. \ máx.})$, que, por sua, vez é determinada pela fórmula:

$$F_{c. \ máx} = 220 - idade$$

em que a idade é dada em ano e $F_{c. max}$, é dado em $bpm$ (batimento por minuto).

Os trechos do percurso nos quais esse ciclista se ,mantém dentro de sua faixa aeróbica ideal, para o ganho de concionamento físico, são: