EN 2022 Matemática - Questões
Abrir Opções Avançadas
Seja $𝐴$ o conjunto de valores reais para o qual $𝑓(𝑥) = \log_{10}[ {\log_{\frac{1}{3}}{(x^2 - x + 1)} } ]$ esteja definida. Seja $B$ o conjunto dos valores reais de $k$ de forma que a equação $x^2 − 2x + \log_{10}{(k − 2)} = 0$ admita raízes reais distintas. Desse modo, assinale a opção que apresenta o conjunto $𝐴 \cap 𝐵$.
Seja a função $f$ definida por $f(t-a) = \begin{cases} 0{,} &0\leq t < a \\ 1, & t \geq a \end{cases}$. Considere o esboço do gráfico de $g$ representado pela figura abaixo.
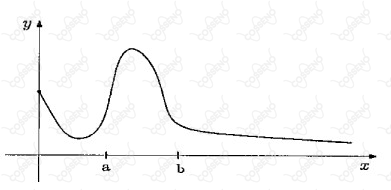
Assinale a opção que apresenta o esboço da parte positiva do gráfico de $g(t-a) f(t-a) - g(t-a) f(t-b)$.
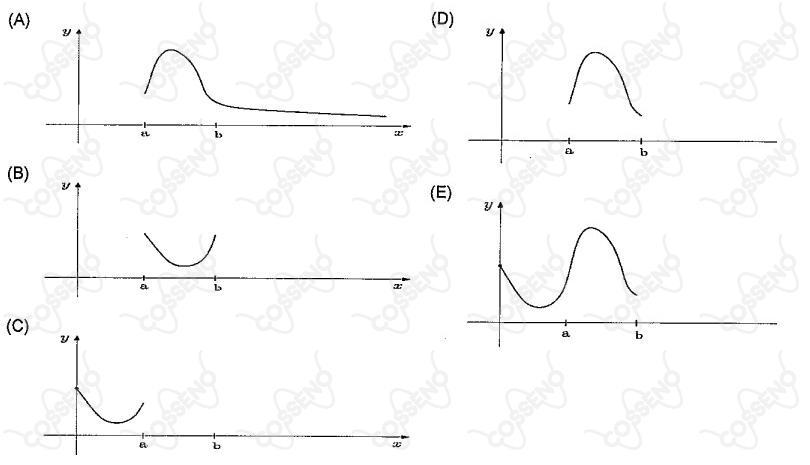
Para que os valores reais de $x$, a sequência geométrica $\left( \frac{2x}{3x + 1}; \frac{2x}{(3x+1)^2}; \frac{2x}{(3x + 1)^3}; ... \right)$ possui o limite da soma de seus termos iguais a $\frac{2}{3}$ ?
Seja $f$ uma função definida no conjunto dos números reais. Supondo que $\displaystyle\lim_{x\to 0}\frac{f(x)}{x} = L$, é correto afirmar que o valor do $\displaystyle\lim_{x\to 1}\frac{f(x^2-1)}{x-1}$ é igual a:
Um ângulo agudo de um triângulo retângulo $ABC$, reto em $C$,é igual a $\alpha$. Sabe-se que a hipotenusa desse triângulo e os prolongamentos de $CA$ e $CB$ são tangentes a uma circunferência de raio $R$. Desse modo, o comprimento da hipotenusa é igual a:
Carregando...