EN 2021 Física - Questões

Em relação ao Eletromagnetismo, assinale a opção INCORRETA.

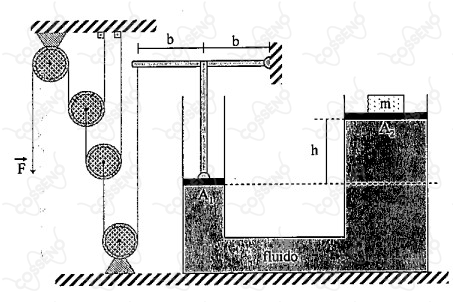
Observe a figura abaixo:

Dois tubos cilíndricos interligados estão cheios de um fluido incompressível de densidade $\rho = 800 \ kg/m^3$. As áreas das faces dos êmbolos são $A_1 = 100 \ cm^2$ e $A_2 = 200 \ cm^2$. Uma haste articulada, de comprimento $2b$, está ligada a um suporte vertical, ambos de massas desprezíveis. O suporte é capaz de se movimentar verticalmente pressionando o êmbolo de área $A_1$ conforme a figura. À esquerda na figura, temos um sistema de roldanas, consideradas ideais com fios ideais. Calcule o módulo da força $F$, em Newtons, para a situação de equilíbrio da figura, considerando a diferença de altura $h = 50,0 \ cm$, $g = 10,0 \ m/s^2$ e $m= 240 \ kg$ e assinale a opção correta.

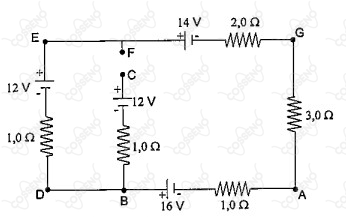
Considere o circuito elétrico esquematizado na figura abaixo. Sabendo que os pontos $F$ e $C$ são mantidos em aberto, calcule a diferença de potencial entre os pontos $G$ e $C$ ($V_G - V_C$) e assinale a opção correta.

Uma prancha de surf, de $1 \ m^2$ de área e $10 \ cm$ de altura, flutua na água com uma parte submersa de altura igual a $2 \ cm$. Considerando a prancha como um paralelepípedo retangular, calcule a altura da parte submersa da prancha, em $cm$, quando um surfista de $70 \ kg$ está sobre ela, e assinale a opção correta, sabendo que a situação descrita ocorre em águas paradas e a prancha permanece sempre na horizontal.

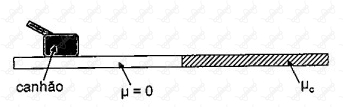
Conforme a figura abaixo, um canhão, inicialmente parado sobre uma superfície sem atrito, aponta numa direção que forma um ângulo de $60^\circ$ com a horizontal e atira uma bala de $60 \ kg$, cuja velocidade na boca do canhão é de $400 \ m/s$. A massa do canhão é de $1000 \ kg$. Após o tiro, o canhão desliza sobre a superfície sem atrito e depois entra em uma região com coeficiente de atrito cinético $\mu_c =0,60$. De acordo com os dados, calcule a distância, em metros, percorrida pelo canhão, na região com atrito, até chegar ao repouso.