CN 2015 - Questões

Considere que N seja um número natural formado apenas por 200 algarismos iguais a 2, 200 algarismos iguais a 1 e 2015 algarismos iguais a zaro. Sobre N, pode-se afirmar que:

A equação $x^3-2x^2-x+2=0$ possui três raízes reais. Sejam $p$ e $q$ números reais fixos, onde $p$ é não nulo. Trocando $x$ por $py+q$, a quantidade de soluções reais da nova equação é:

A solução real da equação $\sqrt{x+4}+\sqrt{x-1}=5$ é:

Sabendo que $2014^4=16452725990416$ e que $2014^2=4056196$, calcule o resto da divisão de $16452730046613$ por $4058211$, e assinale a opção correta.

Observe a figura a seguir.

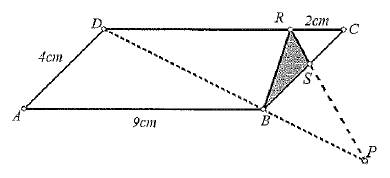
Na figura, o paralelogramo $ABCD$ tem lados $9\ \text{cm}$ e $4\ \text{cm}$. Sobre o lado $\overline{CD}$ está marcado o ponto $R$, de modo que $\overline{CR}=2\ \text{cm}$; sobre o lado $\overline{BC}$ está marcado o ponto $S$ tal que a que a área do triângulo $BRS$ seja $\dfrac{1}{36}$ da área do paralelogramo; e o ponto $P$ é a interseção do prolongamento do segmento $\overline{RS}$ com o prolongamento da diagonal $\overline{DB}$. Nessas condições, é possível concluir que a razão entre as medidas dos segmentos de reta $\dfrac{\overline{DP}}{\overline{BP}}$ vale: