AFA 2021 - Questões

Considere um circuito ôhmico com capacitância e autoindução desprezíveis. Através de uma superfície fixa delimitada por este circuito (Figura 1) aplica-se um campo magnético $\vec{B}$ cuja intensidade varia no tempo $t$ de acordo com o gráfico mostrado.

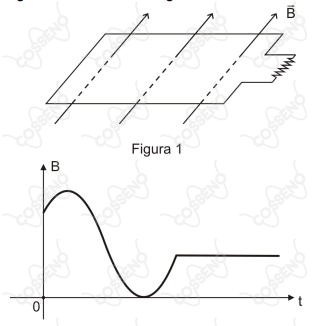
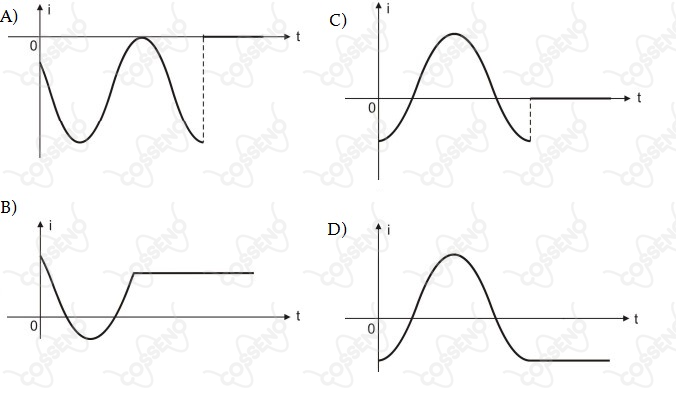
Nessas condições, a corrente induzida $i$ no circuito esquematizado na Figura 1, em função do tempo $t$, é melhor representada pelo gráfico

O ozônio $\ce{(O3)}$ é naturalmente destruído na estratosfera superior pela radiação proveniente do Sol. Para cada molécula de ozônio que é destruída, um átomo de oxigênio $\ce{(O)}$ e uma molécula de oxigênio $\ce{(O2)}$ são formadas, conforme representado abaixo:$$\ce{O3 ->[\downdownarrows{radiação}] O2 + O}$$ Sabendo-se que a energia de ligação entre o átomo de oxigênio e a molécula $\ce{O2}$ tem módulo igual a $\pu{3,75 eV}$, então o comprimento de onda dos fótons da radiação necessária para quebrar uma ligação do ozônio e formar uma molécula $\ce{O2}$ e um átomo de oxigênio vale, em $\pu{nm}$,

Uma partícula de massa $M$ é lançada obliquamente com sua velocidade inicial $\vec{v}_0$ fazendo um ângulo de $30^\circ$ com a direção horizontal, conforme indica figura a seguir.

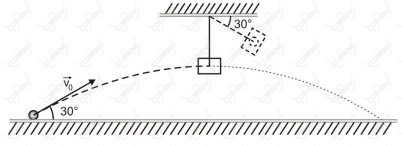
Ao atingir a altura máxima de sua trajetória parabólica, essa partícula colide inelasticamente com um bloco de massa $5M$. Esse bloco, de dimensões desprezíveis, está preso ao teto por um fio ideal, de comprimento $\pu{1,2 m}$, formando um pêndulo balístico. Inicialmente o fio do pêndulo está na vertical. Após a colisão, o pêndulo atinge uma altura máxima, na qual o fio tem uma inclinação de $30^\circ$ em relação à direção horizontal. Desprezando a resistência do ar, o módulo da velocidade inicial da partícula, $v_0$, em $\pu{m/s}$, é igual a

Duas partículas idênticas, $A$ e $B$, se movimentam ao longo de uma mesma trajetória $x$, sendo suas posições, em função do tempo, dadas por $x_A = 2t$ e $x_B = 4 + t$, respectivamente, com $x$ em metros e $t$ em segundos. Em determinado instante, as partículas, que formam um sistema isolado, sofrem uma colisão parcialmente elástica, com coeficiente de restituição $e = 0{,}5$. Nessas condições e desprezando o deslocamento dessas partículas durante a colisão, quando a partícula $A$ estiver na posição $\pu{28 m}$, a partícula $B$ estará na posição, em $\pu{m}$,

Um sistema massa-mola é composto de uma mola ideal de constante elástica $k$ e de um recipiente, de volume interno $V$ e massa desprezível, que é totalmente preenchido com um líquido homogêneo $X$ de densidade constante e desconhecida. Verifica-se que, ao se colocar esse primeiro sistema para oscilar, seu período de oscilação se iguala ao período de oscilação de um segundo sistema, formado de um pêndulo simples de comprimento $L$ e massa $m$. Considere que os dois sistemas oscilam em movimento harmônico simples em um local em que a aceleração gravitacional vale $g$; e que o recipiente preenchido pelo líquido comporte-se como uma massa pontual. Nessas condições, a densidade do líquido $X$ pode ser expressa por