AFA 2020 Física - Questões

Em um local onde a aceleração da gravidade é $g$, as partículas idênticas, $1$ e $2$, são lançadas simultaneamente, e sobem sem atrito ao longo dos planos inclinados $AC$ e $BC$, respectivamente, conforme figura a seguir.

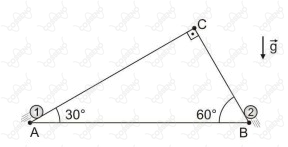
A partícula $2$ é lançada do ponto $B$ com velocidade $v_0$ e gasta um tempo $t$ para chegar ao ponto $C$

Considerando que as partículas $1$ e $2$ colidem no vértice $C$, então a velocidade de lançamento da partícula $1$ vale

A figura a seguir, em que as polias e os fios são ideais, ilustra uma montagem realizada num local onde a aceleração da gravidade é constante e igual a g, a resistência do ar e as dimensões dos blocos $A, B, C$ e $D$ são desprezíveis.

O bloco $Bd$ desliza com atrito sobre a superfície de uma mesa plana e horizontal, e o bloco $A$ desce verticalmente com aceleração constante de módulo $a$.

O bloco $C$ desliza com atrito sobre o bloco $B$, e o bloco $D$ desce verticalmente com aceleração constante de módulo $2a$.

As massas dos blocos $A, B$ e $D$ são iguais, e a massa do bloco $C$ é o triplo da massa do bloco $A$. Nessas condições, o coeficiente de atrito cinético, que é o mesmo para todas as superfícies em contato, pode ser expresso pela razão

Certo brinquedo de um parque aquático é esquematizado pela figura a seguir, onde um homem e uma boia, sobre a qual se assenta, formam um sistema, tratado como partícula.

Essa “partícula” inicia seu movimento do repouso, no ponto $A$, situado a uma altura $H = 15m$, escorregando ao longo do toboágua que está inclinado de $60º$ em relação ao solo, plano e horizontal.

Considere a aceleração da gravidade constante e igual a $g$ e despreze as resistências do ar, do toboágua e os efeitos hidrodinâmicos sobre a partícula. Para freá-la, fazendo-a chegar ao ponto $C$ com velocidade nula, um elástico inicialmente não deformado, que se comporta como uma mola ideal, foi acoplado ligando essa partícula ao topo do toboágua.

Essa circunstância, a deformação máxima sofrida pelo elástico foi de $10\sqrt{2}m$.

Na descida, ao passar pelo ponto $B$, que se encontra uma altura $\frac{H}{2}$, a partícula atinge sua velocidade máxima, que, em $m/s$, vale

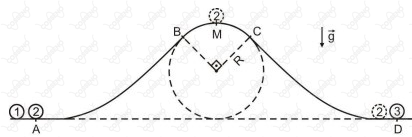
A partícula $1$, no ponto $A$, sofre uma colisão perfeitamente elástica e faz com que a partícula $2$, inicialmente em repouso, percorra, sobre uma superfície, a trajetória $ABMCD$, conforme figura a seguir.

O trecho $BMC$ é um arco de $90º$ de uma circunferência de raio $R = 1,0 m$.

Ao passar sobre o ponto $M$, a partícula $2$ está na iminência de perder o contato com a superfície. A energia mecânica perdida, devido ao atrito, pela partícula $2$ ao longo do trecho $ABM$ é exatamente igual à que ela perde no trecho $MCD$. No ponto $D$, a partícula $2$ sofre outra colisão, perfeitamente elástica, com a partícula $3$, que está em repouso.

As partículas $1$ e $3$ possuem mesma massa, sendo a massa de cada uma delas o dobro da massa da partícula $2$.

A velocidade da partícula $1$, imediatamente antes da colisão no ponto $A$, era de $6,0 m/s$. A aceleração da gravidade é constante e igual a $g$. Desprezando a resistência do ar, a velocidade da partícula $3$, imediatamente após a colisão no ponto $D$, em $m/s$, será igual a

Um pequeno tubo de ensaio, de massa $50 g$, no formato de cilindro, é usado como ludião – uma espécie de submarino miniatura, que sobe e desce, verticalmente, dentro de uma garrafa cheia de água.

A figura $1$, a seguir, ilustra uma montagem, onde o tubo, preenchido parcialmente de água, é mergulhado numa garrafa pet, completamente cheia de água. O tubo fica com sua extremidade aberta voltada para baixo e uma bolha de ar, de massa desprezível, é aprisionada dentro do tubo, formando com ele o sistema chamado ludião. A garrafa é hermeticamente fechada e o ludião tem sua extremidade superior fechada e encostada na tampa da garrafa.

Uma pessoa, ao aplicar, com a mão, uma pressão constante sobre a garrafa faz com que entre um pouco mais de água no ludião, comprimindo a bolha de ar. Nessa condição, o ludião desce, conforme figura $2$, a partir do repouso, com aceleração constante, percorrendo $60 cm$, até chegar ao fundo da garrafa, em $1,0 s$. Após chegar ao fundo, estando o ludião em repouso, a pessoa deixa de pressionar a garrafa. A bolha expande e o ludião sobe, conforme figura $3$, percorrendo os $60 cm$ em $0,5 s$.

Despreze o atrito viscoso sobre o ludião e considere que, ao longo da descida e da subida, o volume da bolha permaneça constante e igual a $V_0$ e $V$, respectivamente. Nessas condições, a variação de volume, $∆V = V − V0$ , em $cm^3$ , é igual a