AFA 2013 Física - Questões

Sejam três vetores $\vec{A}, \vec{B}$ e $\vec{C}$. Os módulos dos vetores $\vec{A} e \vec{B}$ são, respectivamente, $6u$ e $8u$. O módulo do vetor $\vec{S}=\vec{A}+\vec{B}$ vale $10u$, já o módulo do vetor $\vec{D}=\vec{A}+\vec{C}$ é nulo. Sendo o vetor $\vec{R}=\vec{B}+\vec{C}$, tem-se que o módulo de $\vec{F}=\vec{S}+\vec{R}$ é igual a

A figura 1 abaixo apresenta um sistema formado por dois pares de polias coaxiais, $AB$ e $CD$, acoplados por meio de uma correia ideal e inextensível e que não desliza sobre as polias $C$ e $B$, tendo respectivamente raios $R_A = \pu{1 m}, R_B=\pu{2 m},R_C=\pu{10 m}$ e $R_D=\pu{0,5 m}$.

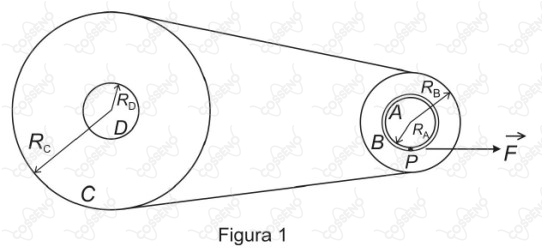
A polia A tem a forma de um cilindro no qual está enrolado um fio ideal e inextensível de comprimento $L = 10\pi\ \pu{m}$ em uma única camada, como mostra a figura 2.

Num dado momento, a partir do repouso, o fio é puxado pela ponta $P$, por uma força $\vec{F}$ constante que imprime uma aceleração linear a, também constante, na periferia da polia $A$, até que o fio se solte por completo desta polia. A partir desse momento, a polia $C$ gira até parar após $n$ voltas, sob a ação de uma aceleração angular constante de tal forma que o gráfico da velocidade angular da polia $D$ em função do tempo é apresentado na figura 3.

Nessas condições, o número total de voltas dadas pela polia $A$ até parar e o módulo da aceleração a, em $\pu{m/s^2}$, são, respectivamente, em função do tempo é apresentado na figura 3.

Duas partículas, a e b, que se movimentam ao longo de um mesmo trecho retilíneo tem as suas posições (S) dadas em função do tempo (t), conforme o gráfico abaixo.

O arco de parábola que representa o movimento da partícula b e o segmento de reta que representa o movimento de a tangenciam-se em $t = \pu{3 s}$. Sendo a velocidade inicial da partícula $b$ de $\pu{8 m/s}$, o espaço percorrido pela partícula a do instante $t = O$ até o instante $t = \pu{4 s}$, em metros, vale

Uma pequena esfera de massa m é mantida comprimindo uma mola ideal de constante elástica k de tal forma que a sua deformação vale x. Ao ser disparada, essa esfera percorre a superfície horizontal até passar pelo ponto A subindo por um plano inclinado de 45º e, ao final dele, no ponto B, é lançada, atingindo uma altura máxima $H$ e caindo no ponto $C$ distante $3h$ do ponto $A$, conforme figura abaixo.

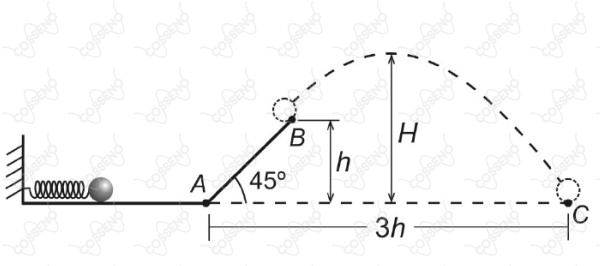
Considerando a aceleração da gravidade igual a $g$ e desprezando quaisquer formas de atrito, pode-se afirmar que a deformação $x$ é dada por

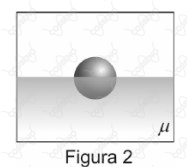
Uma esfera homogênea, rígida, de densidade $\mu _1$ e de volume $V$ se encontra apoiada e em equilíbrio na superfície inferior de um recipiente, como mostra a figura 1. Nesta situação a superfície inferior exerce uma força $N_1$ sobre a esfera.

A partir dessa condição, o recipiente vai sendo preenchido lentamente por um líquido de densidade $\mu$, de tal forma que esse líquido esteja sempre em equilíbrio hidrostático. Num determinado momento, a situação de equilíbrio do sistema, no qual a esfera apresenta metade de seu volume submerso, é mostrada na figura 2.

Quando o recipiente é totalmente preenchido pelo líquido, o sistema líquido-esfera se encontra em uma nova condição de equilíbrio com a esfera apoiada na superfície superior do recipiente (figura 3), que exerce uma força de reação normal $N_2$ sobre a esfera.

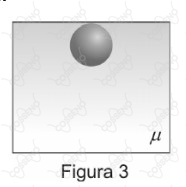
Nessas condições, a razão $\frac{N_2}{N_1}$ é dada por