AFA 2012 - Questões
Abrir Opções Avançadas
Considere $ f $ uma função quadrática de raízes reais e opostas. O gráfico de $ f $ intercepta o gráfico da função real g definida por $ g(x)=-2 $ em exatamente um ponto.
Se $ f(\sqrt{3})=4 $ e $ D(f) = D(g) = \mathbb{R} $, então, é INCORRETO afirmar que
Considere a função real $ g:A \rightarrow \mathbb{R} $ tal que $ g(x)=\frac{x^2-x}{x^2+x} $
Sabendo-se que o conjunto A é o mais amplo possível, é verdade que
Sejam $ (1, a_2, a_3, a_4) $ e $ (1, b_2, b_3, b_4) $ uma progressão aritmética e uma progressão geométrica, respectivamente, ambas com a mesma soma dos termos e ambas crescentes. Se a razão $ r $ da progressão aritmética é o dobro da razão $ q $ da progressão geométrica, então, o produto $ r.q $ é igual a
Considere A o conjunto mais amplo possível na função real $ f:A \rightarrow \mathbb{R} $, dada por $ f(x)=\frac{\sin x}{\csc x} + \frac{\cos x}{\sec x} $
Sobre a função f é correto afirmar que
Um sólido maciço foi obtido quando a base de uma pirâmide hexagonal regular de altura $ \pu{6 cm} $ foi colada à base de uma pirâmide reta de base retangular e altura $ \pu{3 cm} $, de forma que 4 dos 6 vértices da base da primeira coincidam com os vértices da base da segunda, conforme figura.
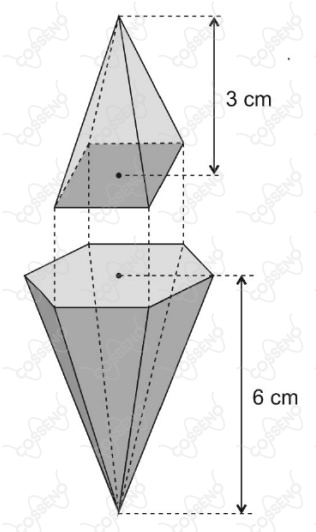
Desprezando-se o volume da cola, se a aresta da base da pirâmide hexagonal mede $ \pu{\sqrt{5} cm} $, então, o volume do sólido obtido, em $ \pu{cm3} $, é igual a
Carregando...