AFA 2005 - Questões

Filtro de Questões

Abrir Opções Avançadas

Filtrar por resolução:

01 AFA 2005 - Matemática

Dados os conjuntos $A$ e $B$, tais que $$A = \{ (x, y) \in \mathbb{R}^{2} \space | \space x^{2} + y^{2} \leq 9 \} \\ B = \{ (x, y) \in \mathbb{R}^{2} \space | \space x - y \leq m, m \in \mathbb{R} \}$$ É correto afirmar que

$A$ e $B$ são disjuntos se $m = -3 \sqrt{2}$

$A$ é subconjunto de $B$ se $|m| < 3 \sqrt{2}$

$A \cap B \neq \varnothing$ se $m \geq 3\sqrt{2}$

$A$ e $B$ nunca terão apenas um ponto comum.

02 AFA 2005 - Matemática

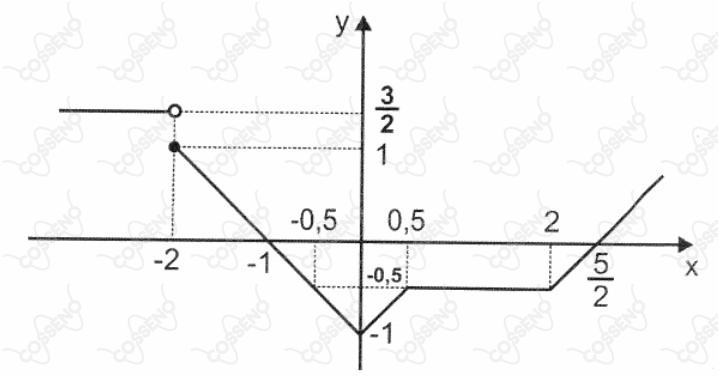
Seja $f$ a função real cujo gráfico se apresenta a seguir:

Analisando o gráfico, é $INCORRETO$ afirmar que

$f(f(1)) = f(0,5)$

$f(0) \leq f(x), \space \forall \space x \in \mathbb{R}$

$f(0) + 1 > 0, \space \forall x \in \mathbb{R}$

se $g(x) = f(x) - 1$, então $g(-2)= f\left( \frac{5}{2} \right )$

03 AFA 2005 - Matemática

Considere $P_{1}$, $P_{2}$, $P_{3}$, $P_{4}$, $\cdots$, $P_{n}$ os $n$ primeiro números naturais primos consecutivos com $n \geq 5$. Se $x = P_{1} \cdot P_{2}^{2} \cdot P_{3}^{3} \cdot P_{4}^{4} \cdot \space \cdots \space \cdot P^{n}_{n}$ e $y = P_{1} \cdot P_{2} \cdot P_{3} \cdot P_{4} \cdot \space \cdots \space \cdot P_{n}$, então o número total de divisores positivos de $\frac{x}{y}$ é dado por

$(n + 1)!$

$n! + 1$

$n!$

$(n -1)!$

04 AFA 2005 - Matemática

Dada a função real $f$ definida por $f(x) = x^{2}$, considere a função real $g$ definida por $g(x) = f(x + m) + k$, sendo $m \space e \space k \in \mathbb{R}$.

É $\text{INCORRETO}$ afirmar que

o gráfico da função g em relação ao gráfico da função $f$ é deslocado $k$ unidades para cima, se $k > 0$, e $m$ unidades para a direita, se $m < 0$

se $m = 0$ e $k = 1$, então o conjunto imagem de $g$ é dado por $Im = \{ y \in \mathbb{R} \space | \space y \geq 1 \}$

a equação do eixo de simetria da parábola que representa $g$ é dada por $x = m$

se $m = -2$ e $k = -3$, então as coordenadas do vértice da parábola que representa $g$ são $(-m, k)$

05 AFA 2005 - Matemática

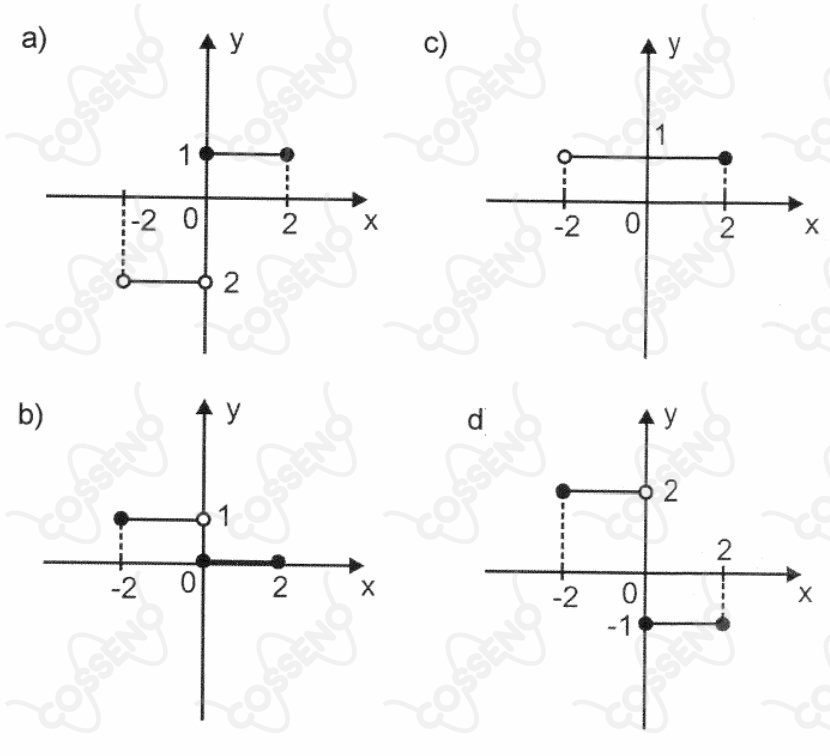
Considere a função $f(x) = \begin{cases} 1, \space se \space 0 \leq x \leq 2 \\ -2, \space se \space -2 \leq x < 0 \end{cases}$. A função $g(x) = |f(x)| - 1$ terá o seguinte gráfico:

Carregando...