Um circuito elétrico é composto por uma bateria ideal com uma tensão de , resistores cada qual com uma resistência elétrica de , fios condutores ideais e duas chaves que permitem abrir ou fechar o circuito ou parte dele.
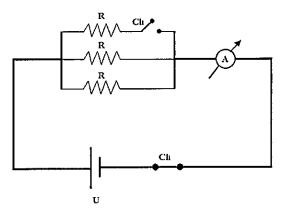
Além disso, conta com um amperímetro ideal . Na situação apresentada na figura, qual das opções fornece, respectivamente, a resistência elétrica equivalente do circuito e a intensidade da corrente elétrica indicada pelo amperímetro?
CossenoGPT
Teste
gratuitamente agora
mesmo! 

Para resolver essa questão precisamos perceber que a resistência elétrica do resistor na parte superior(local em que a chave abre uma parte do circuito) não será considerado em relação ao cálculo da resistência equivalente $R_{eq}$ , justamente por que a chave abre essa parte do circuito elétrico, dessa forma deveremos considerar apenas a resistência elétrica dos resistores restantes para o cálculo da resistência equivalente $R_{eq}$.
$\therefore$
$\dfrac{1}{R_{eq}} = \dfrac{1}{R} + \dfrac{1}{R} = \dfrac{1}{3\Omega} + \dfrac{1}{3\Omega} = \dfrac{2}{3\Omega} \implies R_{eq} = \dfrac{3}{2}\Omega = \boxed{R_{eq} = 1,5\Omega} $
Agora iremos analisar o sentido da corrente elétrica $i$ e o percurso dessa corrente até chegar ao amperímetro e depois calcular a intensidade da corrente elétrica ao final desse percurso. Pelo fato de a bateria ser um gerador elétrico , temos que a corrente elétrico dirige-se do polo negativo para o positivo no gerador, quando a corrente elétrica chegar ao ponto de bifurcação na associação de resistores em paralelo , a corrente elétrica não será dividida com a parte em que está presente a chave(que abre essa parte do circuito) , concluindo que essa corrente será divida apenas com as partes restantes , quando essas divisórias de corrente elétrica se juntam , a intensidade de corrente elétrica resultante será igual a $|i|$ , logo , ao final desse percurso a corrente elétrica $i$ não se alterou e por conclusão o amperímetro ideal marcará a intensidade de corrente elétrica $|i|$ .
$\therefore$
$| i| = \dfrac{U}{R_{eq}} = \dfrac{15}{1,5}A = \boxed{|i| = 10A}$
$\textbf{Resposta : Letra C }$

