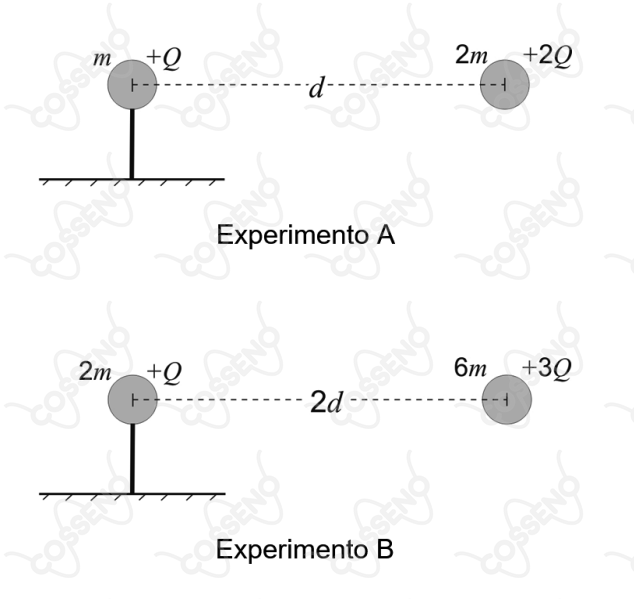
Em dois experimentos, e , uma partícula foi fixada à esquerda e outra partícula à direita foi solta com velocidade nula, conforme geometrias apresentadas nas figuras acima. Em cada experimento, mediu-se a velocidade final que a partícula da direita alcançou muito tempo após ser solta.
Definindo como a velocidade escalar final da partícula solta no experimento e como a velocidade escalar final da partícula solta no experimento , a razão é
Observação:
• os movimentos das partículas nos experimentos ocorrem sempre na horizontal e sem a influência da gravidade.
CossenoGPT
Teste
gratuitamente agora
mesmo! 

Pelo Teorema da Energia Cinética, o trabalho da força resultante é igual à variação da energia cinética. Deste fato, determinemos o trabalho realizado pela força elétrica em cada experimento, encontrando assim a velocidade final de cada partícula.
Se $F_e~=~\dfrac{Q_1 Q_2 K}{x^2}$, sendo esta força variável, o trabalho $W$ realizado pela força elétrica é $\displaystyle{\int_{x}^{0} F_e \,dx}~=~Q_1 Q_2 K\displaystyle{\int_{x}^{0} \dfrac{1}{x^2} \,dx}~=~\dfrac{Q_1Q_2 K}{x}~=~W$. Dessa forma:$$W_A~=~\dfrac{2Q^2 K}{d}~=~\dfrac{2mv_A^2}{2} \implies v_A^2~=~\dfrac{2Q^2 K}{md}$$$$W_B~=~\dfrac{3Q^2 K}{2d}~=~\dfrac{6mv_A^2}{2} \implies v_B^2~=~\dfrac{Q^2 K}{2md}$$Assim$$\left(\dfrac{v_A}{v_B}\right)^2~=~\dfrac{2}{\dfrac{1}{2}}~=~4 \implies \boxed{\dfrac{v_A}{v_B}~=~2}$$$$\bf{Alternativa~(C)}$$

