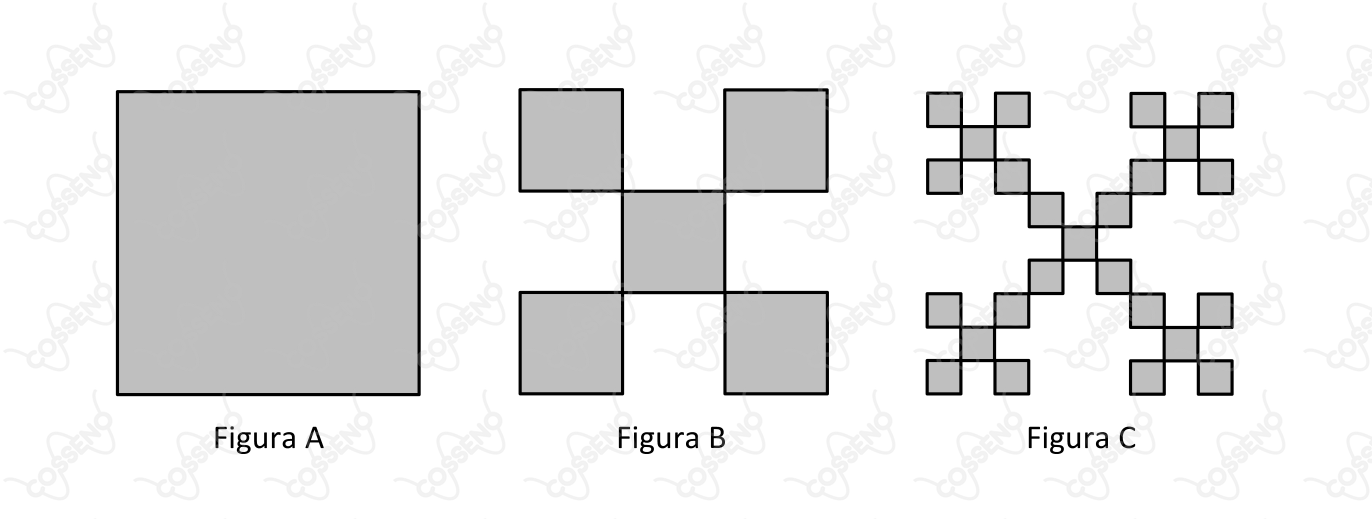
Considere o quadrado de lado apresentado na Figura . Ao aplicar uma determinada operação de corte, obtém-se a Figura e repetindo a operação, em cada quadrado remanescente obtém-se a Figura . Qual será a área remanescente, a partir do quadrado da Figura , ao final de operações?
CossenoGPT
Teste
gratuitamente agora
mesmo! 

Seja $ (A_n) $ a sequência determinada pelas áreas das figuras.
$$
\begin{aligned}
A_1 & = L^2\\
A_2 & = 5 \cdot \left( \frac{L}{3} \right)^2 = \frac{5L^2}{9}\\
A_3 & = 25 \cdot \left( \frac{L}{9} \right)^2 = \frac{25L^2}{9}
\end{aligned}
$$
$(A_n)$ é uma progressão geométrica de razão $ q = \frac{5}{9}$ e de primeiro termo $A_1 = L^2$. Assim, após a décima operação, vamos obter o décimo primeiro elemento da referida sequência:
$$
A_{11} = L^2 \cdot \left( \frac{5}{9} \right)^{10} = \frac{5^{10} L^2}{9^{10}}
$$