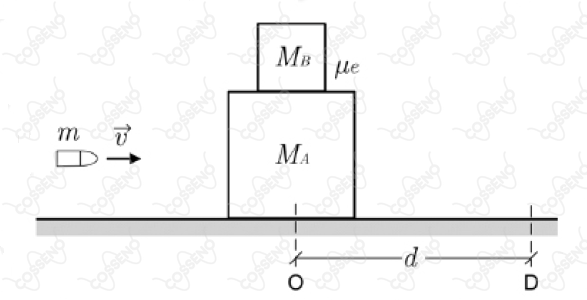
Um projétil de massa é disparado com velocidade contra dois blocos e , de massas e , que estão inicialmente em repouso, um sobre o outro, conforme mostra a figura. O projétil atinge o bloco , fazendo o conjunto se movimentar de uma distância , da posição até a posição . Considerando a aceleração da gravidade local, o coeficiente de atrito estático mínimo entre os blocos, de modo que o bloco não deslize sobre o bloco , é:
CossenoGPT
Teste
gratuitamente agora
mesmo! 

Entende-se, pelo enunciado, que a colisão entre o bloco A e o projétil é inelástica.
Depois desta colisão, a tendência do bloco A é se movimentar à direita, tornando, assim, a tendência de deslizamento do bloco B à esquerda. Por conta disso, a superfície do bloco A exercerá uma força de atrito em B, à direita, e do mesmo modo haverá uma reação em A, só que à esquerda, contrária ao seu movimento. É isto que fará com que A freie no ponto D.$$\mu\cdot F_n \geq F_{at} \implies \mu = \frac{F}{F_n}$$Em que $F_{at}$ é força de atrito, $F$ é a força de atrito máxima, $\space F_n$ é a força normal e $\mu$ é o coeficiente de atrito estático mínimo, o qual a questão procura.
A força de atrito máxima para que o bloco B não deslize será de $F = M_B\mu g = M_B a$, assim $a = \mu g$, sendo $a$ a desaceleração por B gerada.
Pela conservação da quantidade de movimento, a velocidade inicial do conjunto, $v_c$ é:$$m\cdot v = 1000m\cdot v_c \implies v_c = \frac{v}{10^3}$$Pela equação de Torricelli, portanto:$$v_c^2 = 2\cdot a\cdot d \implies \frac{v^2}{10^6} = 2\cdot \mu g \cdot d \implies \boxed{\mu = \frac{v^2}{2\cdot 10^6 gd}}$$

