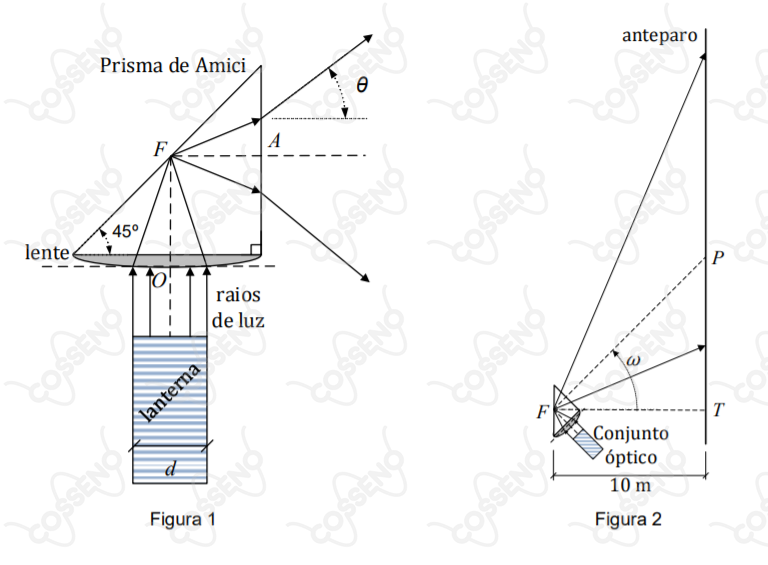
Um conjunto óptico é formado por uma lente convergente e um prisma de Amici, conforme mostra a Figura $1$. O conjunto está totalmente integrado, sendo formado pelo mesmo vidro. A lente possui centro óptico $O$ e foco $F$ situado sobre a face-hipotenusa do prisma. Nesse prisma, os raios incidentes sobre a face-hipotenusa sofrem reflexão interna total. Uma lanterna cilíndrica muito potente, com potência óptica de $P = \pi \sqrt{3} \ W$ e diâmetro $d = 10 \ cm$, gera raios de luz paralelos ao eixo principal da lente. A lanterna está solidária ao sistema óptico e seus raios são focalizados pela lente e refletidos pelo prisma, até a sua face-cateto plana, saindo do prisma e projetando a luz sobre um anteparo plano alinhado verticalmente. Conforme mostra a Figura $2$, no intervalo $0 \leq t < 12 \ s$, todo o conjunto óptico começa a girar, a partir do instante em que $P$ coincide com $T$, em velocidade angular constante $\omega = \pi/36 \ rad/s$. Dessa forma, o contorno da luz projetada no anteparo passa a ser uma curva plana, conhecida na matemática.
Diante do exposto, determine:
a) o ângulo de abertura $\theta$ do cone formado na saída do prisma, quando o índice de refração do conjunto óptico é o mínimo para que o feixe luminoso seja totalmente refletido na face-hipotenusa;
b) a expressão da velocidade escalar $v(t)$ com que o ponto $P$ (interseção do eixo do cone com o anteparo) desloca-se verticalmente ao longo do anteparo; e
c) a densidade de potência, em $W/m^{2}$, da luz projetada no anteparo, em $t = 9 \ s$. Neste caso, considere que todas as dimensões do prisma são muito pequenas em relação à distância para o anteparo, ou seja, o ângulo de abertura é $\theta$ ao longo de todo o cone de saída, a partir de $F$.
- o meio externo é o ar: $n_{1} = 1$;
- $\overline{OF} = \overline{FA} = 5(1 + 2 \sqrt{2}) \ cm$; e
- a separação horizontal entre o foco $F$ da lente e o anteparo$,$ no ponto $T,$ é $\overline{FT} = 10 \ m$.
Observação:
- a linha $\overline{FP},$ prolongamento de $\overline{FA},$ é o eixo do cone;
- o ângulo $\theta$ é o ângulo entre o eixo e qualquer geratriz do cone de luz de saída do prisma; e
- desconsidere qualquer perda da intensidade luminosa ao longo de todo o percurso até o anteparo.
CossenoGPT

