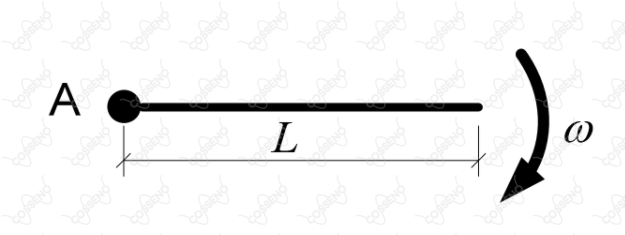
Uma corda de comprimento e densidade linear constante gira em um plano em torno da extremidade fixa no ponto a uma velocidade angular constante igual a . Um pulso ondulatório é gerado a partir de uma das extremidades. A velocidade do pulso, no referencial da corda, a uma distância da extremidade fixa é dada por
CossenoGPT
Teste
gratuitamente agora
mesmo! 

Para calcular a velocidade dos pulsos ondulatórios em cordas vibrantes, usamos a equação de Taylor:$$v=\sqrt{\dfrac{T}{\mu}}$$Onde $v$ é a velocidade do pulso, $T$ é a tensão na corda e $\mu$ é a densidade linear da corda (massa por comprimento).
Agora, para este problema, como determinamos a tensão da corda?
Pela segunda lei de Newton, podemos afirmar que o ponto da corda a uma distância $r$ do centro de rotação tem resultante centrípeta $F_{cp}$. Mas por ser adimensional, não podemos simplesmente dizer que essa força é $m\cdot a$: precisamos tomar proveito da extensão da corda para expressar "massas que aceleram", ou seja, cuja força conseguimos calcular.
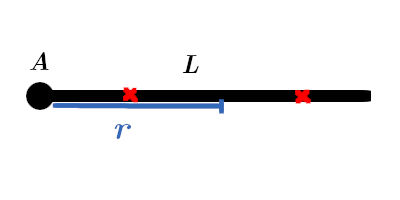 Em concreto, podemos dizer que esse ponto é "puxado" pelo pedaço de corda à sua esquerda e pelo pedaço de corda à sua direita. No desenho acima, representados a vermelho, estão os centros de massa desses pedaços de corda.
A tensão com que o pedaço à esquerda puxa o ponto é dada por:$$T_1=F_{\text{res }1}\\T_1=m\cdot a_{cp}=\mu r\cdot \omega^2\frac{r}{2} = \boxed{\mu\frac{\omega^2r^2}{2}}$$Já o pedaço da direita, ao mesmo tempo que puxa o ponto, também é puxado pelo pedaço da esquerda com a mesma tensão $F_1$. A resultante das forças nesse pedaço é igual a:$$\begin{align}F_{\text{res} 2}&=T_2 - T_1\\ma_{cp}&=T_2 - T_1\\ T_2 &= ma_{cp}+T_1\\T_2 &= \left(\mu(L-r)\cdot \omega^2\frac{L+r}{2}\right) + T_1\\ T_2&=\boxed{\mu\omega^2\left(\frac{L^2-r^2}{2}\right)+T_1}\end{align}$$E enfim, podemos escrever que a força resultante para o ponto a uma distância $r$ do eixo de rotação da corda é igual a: $$\begin{align}F_\text{res}&=T_2 - T_1\\F_\text{res}&=\mu\omega^2\left(\frac{L^2-r^2}{2}\right)+T_1-T_1\\F_\text{res}&=\boxed{\mu\omega^2\left(\frac{L^2-r^2}{2}\right)}\end{align}$$Então, substituindo a tensão resultante na equação de Taylor para encontrar a velocidade do pulso:$$v=\sqrt{\omega^2\left(\frac{L^2-r^2}{2}\right)}\\\boxed{v=\omega\sqrt{\frac{L^2-r^2}{2}}\quad\text{Gab. D)}}$$
Em concreto, podemos dizer que esse ponto é "puxado" pelo pedaço de corda à sua esquerda e pelo pedaço de corda à sua direita. No desenho acima, representados a vermelho, estão os centros de massa desses pedaços de corda.
A tensão com que o pedaço à esquerda puxa o ponto é dada por:$$T_1=F_{\text{res }1}\\T_1=m\cdot a_{cp}=\mu r\cdot \omega^2\frac{r}{2} = \boxed{\mu\frac{\omega^2r^2}{2}}$$Já o pedaço da direita, ao mesmo tempo que puxa o ponto, também é puxado pelo pedaço da esquerda com a mesma tensão $F_1$. A resultante das forças nesse pedaço é igual a:$$\begin{align}F_{\text{res} 2}&=T_2 - T_1\\ma_{cp}&=T_2 - T_1\\ T_2 &= ma_{cp}+T_1\\T_2 &= \left(\mu(L-r)\cdot \omega^2\frac{L+r}{2}\right) + T_1\\ T_2&=\boxed{\mu\omega^2\left(\frac{L^2-r^2}{2}\right)+T_1}\end{align}$$E enfim, podemos escrever que a força resultante para o ponto a uma distância $r$ do eixo de rotação da corda é igual a: $$\begin{align}F_\text{res}&=T_2 - T_1\\F_\text{res}&=\mu\omega^2\left(\frac{L^2-r^2}{2}\right)+T_1-T_1\\F_\text{res}&=\boxed{\mu\omega^2\left(\frac{L^2-r^2}{2}\right)}\end{align}$$Então, substituindo a tensão resultante na equação de Taylor para encontrar a velocidade do pulso:$$v=\sqrt{\omega^2\left(\frac{L^2-r^2}{2}\right)}\\\boxed{v=\omega\sqrt{\frac{L^2-r^2}{2}}\quad\text{Gab. D)}}$$

Ampliar Imagem
Inicialmente podemos escrever que
$dT = dm \cdot \omega^2 \cdot x$
Normalmente calculamos em $dx$ , mas note que calcular em $dm$ será mais simples para esse caso.
Como temos que $\mu = \dfrac{dm}{dx}$ , então $dm = \mu \cdot dx$
$\therefore$
$dT = dm \cdot \omega^2 \cdot x =dT = \mu \cdot \omega^2 \cdot x $ $dx$
Integrando ambos os lados temos que
$T =\mu \omega^2 \int_{r}^{L}x dx $
$= T = \mu \omega^2 \cdot \dfrac{(L^2 - r^2)}{2}$
A velocidade $v$ desejada é dada pela equação de Taylor $v = \sqrt{\dfrac{T}{\mu}}$
$\therefore$
$v = \sqrt{\dfrac{T}{\mu}} = v = \sqrt{ \omega^2 \cdot \dfrac{(L^2 - r^2)}{2}} = \boxed{v = \omega \sqrt{\dfrac{(L^2 - r^2)}{2}}}$
$\textbf{Resposta : Alternativa D}$



