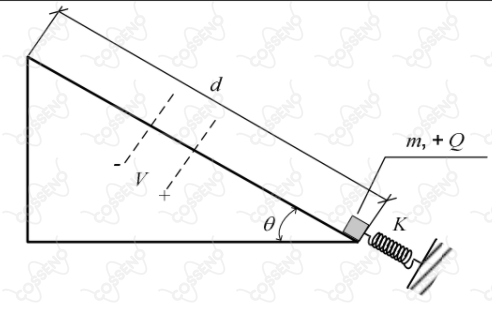
Um corpo de carga positiva, inicialmente em repouso sobre uma rampa plana isolante com atrito, está apoiado em uma mola, comprimindo-a. Após ser liberado, o corpo entra em movimento e atravessa uma região do espaço com diferença de potencial , sendo acelerado. Para que o corpo chegue ao final da rampa com velocidade nula, a distância indicada na figura é
Dados:
• deformação inicial da mola comprimida: $x$;
• massa do corpo: $m$;
• carga do corpo: $+ Q$;
• aceleração da gravidade: $g$;
• coeficiente de atrito dinâmico entre o corpo e a rampa: $\mu$;
• ângulo de inclinação da rampa: $\theta$;
• constante elástica da mola: $K$.
Considerações: • despreze os efeitos de borda; • a carga do corpo permanece constante ao longo da trajetória.
Considerações: • despreze os efeitos de borda; • a carga do corpo permanece constante ao longo da trajetória.
CossenoGPT
Teste
gratuitamente agora
mesmo! 

Analisando o sistema, identificamos que no inicialmente há energia potencial elástica (a mola está comprimida), que será transformada em apenas energia potencial gravitacional, quando o corpo chega no topo da rampa.
Além do impulso que a mola dá inicialmente, o corpo também é "empurrado" para cima pela força elétrica que atua na região da figura onde há diferença de potencial elétrico.
Portanto, nossa estratégia de resolução é usar a conservação de energia para encontrar o comprimento $d$ da rampa que permite que o bloco fique parado ao chegar no topo. E como conservar energia significa que $\Delta E = 0$:$$E_{\text{pot elástica}}+T_{\text{força elétrica}}-E_{\text{pot gravitacional}}-T_{\text{atrito}}=0$$Começando com a energia potencial elástica, como a mola tem deformação inicial $x$:$$E_{\text{pot elástica}}=\dfrac{Kx^2}{2}$$Já o trabalho da força elétrica, pela definição de potencial elétrico, é simplesmente$$T_{\text{força elétrica}}=QV$$Agora, para determinar a energia potencial gravitacional do objeto quando ele está no topo da rampa, precisamos antes saber qual altura $h$ ele subiu. Olhando para o triângulo da figura, podemos afirmar que $\frac{h}{d}=\sin\theta$, e assim, $h=d\sin\theta$. Então a energia potencial gravitacional no topo é apenas:$$E_{\text{pot gravitacional}}=mgh=mgd\sin\theta$$E por último, o módulo do trabalho da força de atrito é igual ao módulo da força de atrito multiplicado pela distância $d$ que o corpo percorreu até o topo. Assim:$$T_{\text{atrito}}=\mu \cdot N\cdot d = \mu \cdot mg\cos\theta\cdot d$$Logo, substituindo tudo na equação de conservação da energia:$$\dfrac{Kx^2}{2}+QV-mgd\sin\theta-\mu mg\cos\theta d=0\\ Kx^2 + 2QV = 2dmg (\sin\theta + \mu\cos\theta)\\\boxed{d=\dfrac{Kx^2+2QV}{2mg(\mu\cos\theta+\sin\theta)}}\Rightarrow\text{Gab. E)}$$

