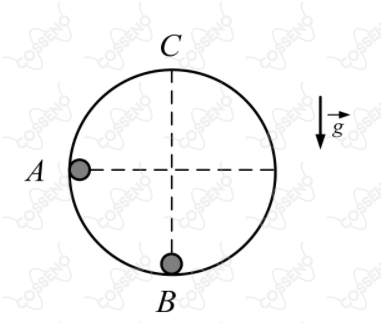
Um corpo puntiforme de massa parte de ponto , percorrendo a rampa circular representada na figura acima, sem atrito, colide com outro corpo puntiforme de massa , que se encontrava inicialmente em repouso no ponto . Sabendo que este choque é perfeitamente inelástico e que o corpo resultante deste choque atinge o ponto , ponto mais alto da rampa, com a menor velocidade possível mantendo o contato com a rampa, a velocidade inicial do corpo no ponto , em , é
raio da rampa circular: $2 m$
aceleração da gravidade $g$ : $10 \ m/{s}^{2}$
massa $m_A = 1 \ kg$
massa $m_B = 1 \ kg$
CossenoGPT
Teste
gratuitamente agora
mesmo! 

As forças atuantes nestes corpos são a Normal e o Peso. A Normal, por sua vez, atua sempre de modo perpendicular à trajetória. Nesse sentido, a única força que realiza trabalho é o Peso, que é uma força conservativa. Então, neste sistema, há conservação da energia mecânica.
Pela conservação da energia, em relação ao corpo em A, temos:$$2\cdot m_A\cdot g + \frac{m_a\cdot v_{ai}^2}{2}= \frac{m_A\cdot v_{af}^2}{2} \implies v_{af} = \sqrt{v_{ai}^2 + 40 \space}$$Em que $v_{af}$ é a velocidade do corpo em A, em $\text{m/s}$, imediatamente antes de colidir com corpo em B, e $v_{ai}$ é a velocidade inicial do corpo em A, a qual, aliás, a questão procura.
Dada a colisão inelástica, pela conservação da quantidade de movimento, temos:$$m_a\cdot v_{af} = (m_a + m_b)\cdot v_{ab} \implies v_{ab} = \frac{\sqrt{v_{ai}^2 + 40 \space}}{2}$$Sendo $v_{ab}$, em $\text{m/s}$, a velocidade do conjunto dos corpos adquirida após a colisão.
Agora, analisemos o equilíbrio das forças no ponto C :$$P + F_n = m\cdot \frac{v^2}{R}$$Em que $P$ é o peso, $F_n$ é a força normal e $\large{\frac{v^2}{R}}$ é a aceleração centrípeta.
A interpretação de se obter a menor velocidade $v$ parte da ideia de minimizarmos a $F_n$, tendendo o módulo desta força a zero $(F_n \approx 0)$. Diante do exposto e das informações do enunciado, temos, de modo aproximado, que:$$P = m\cdot g = m\cdot \frac{v_{min}^2}{R} \implies v_{min} = \sqrt{gR\space} = 2\sqrt{5}$$
Dessa forma, pela conservação da energia mecânica, temos:$$\frac{(m_a+m_b)\cdot v_{ab}^2}{2} = 4\cdot (m_a+m_b)\cdot g \space +\space \frac{(m_a+m_b)\cdot v_{min}^2}{2}$$$$\frac{v_{ai}^2 + 40}{4} = 80 + 20 = 100 \implies \boxed{v_{ai} = 6\sqrt {10}\space \space \text{m/s}}$$
Não há alternativas.

