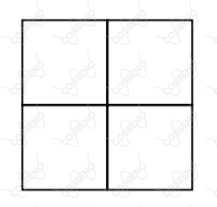
Cada um dos quatro quadrados menores da figura acima é pintado aleatoriamente de verde, azul, amarelo ou vermelho. Qual é a probabilidade de que ao menos dois quadrados, que possuam um lado em comum, sejam pintados da mesma cor?
CossenoGPT
Teste
gratuitamente agora
mesmo! 

Existem duas formas relativamente intuitivas de resolver problemas desse tipo; você pode realizar o processo diretamente ou indiretamente (a partir de probabilidade complementar). Nessa perspectiva, ao analisar a questão, nota-se o interesse de "ao menos dois quadrados", ou seja, a probabilidade completar pode ser bem eficiente, visto que calcular a probabilidade de "sequer dois quadrados de mesma cor" é, aparentemente, mais simples. Enfim, continuemos:
$• \ \text{Resolução I:}$ $\color{#3368b8}{\text{Evento Direto}}$
Comecemos por perceber que colorir ao menos dois quadrados de mesma cor significa, grosso modo, poder colorir mais de dois. Com isso em mente, o mais simples será dividir em casos, faremos substancialmente $3$, são eles:\begin{matrix}
\text{Caso I:}& \text{4 quadrados com a mesma cor} \\
\text{Caso II:}& \text{3 quadrados com a mesma cor} \\
\text{Caso III:}& \text{2 quadrados com a mesma cor}
\end{matrix}Então, pensando no primeiro caso - mais simples por sinal -, tem-se de escolher uma entre quatro cores no intuito de pintar os quatro quadrados. Ora, são $4$ cores possíveis, logo, são quatro eventos possíveis:\begin{matrix}
\#(\text{I}) = \text{4 eventos}
\end{matrix}Já para o segundo caso, deve-se escolher três dos quatro quadrados, ou seja, $C_4^3$. Após isso, deve-se definir uma cor para esses três quadrados, isto é, escolher uma das $4$ opções. Por fim, o último quadrado deve ser de uma cor diferente dos demais, logo, restam-se $3$ opções para o último. Em suma, pelo princípio multiplicativo, constata-se: \begin{matrix}
\#(\text{II}) = C_4^3 \cdot 4 \cdot 3 &\therefore& \#(\text{II}) = \text{48 eventos}
\end{matrix}Agora, pensando no último caso, o problema é um pouco maior. A princípio, deve-se salientar que os quadros devem possuir dois lados comuns, ou seja, há mais três subcasos:\begin{matrix}
\text{Caso III}_1:& \text{2 quadrados na horizontal com a mesma cor} \\
\text{Caso III}_2:& \text{2 quadrados na vertical com a mesma cor} \\
\text{Caso III}_3:& \text{2 quadrados com uma cor e outros 2 com outra} \\
\end{matrix}Repare que o dois primeiros subcasos acima são praticamente análogos, existem $2$ horizontais (verticais) possíveis, e dessas precisamos escolher uma entre $4$ cores. Já para os demais, o terceiro escolhido apresentará $3$ cores possíveis, assim como o último possuirá apenas $2$ - ele precisa ser diferente dos demais. Resumindo, segue:\begin{matrix}
\#(\text{III}_1) = 2 \cdot 4 \cdot 3 \cdot 2 &\therefore& \#(\text{III}_1) = \text{48 eventos} \\
\#(\text{III}_2) = 2 \cdot 4 \cdot 3 \cdot 2 &\therefore& \#(\text{III}_2) = \text{48 eventos}
\end{matrix}No fim, pensando no último subcaso, veja que existem $2$ possibilidades: cores iguais na vertical ou horizontal. Seguindo esse raciocínio, necessita-se escolher uma dentre $4$ cores para dois dos quadrados, assim como uma dentre $3$ cores restantes para os demais. Assim,\begin{matrix}
\#(\text{III}_3) = 2 \cdot 4 \cdot 3 &\therefore& \#(\text{III}_2) = \text{24 eventos}
\end{matrix}Para a probabilidade em questão, resta apenas encontrar o espaço amostral $\#W$, o que não é difícil; só é preciso pensar em todas as formas possíveis de colorir a imagem, isto é, $4^4$. Como resultado, conclui-se:\begin{matrix}
P = \dfrac{\#(\text{I}) + \#(\text{II}) + \#(\text{III}_1) + \#(\text{III}_2) + \#(\text{III}_3) }{\#W}
\end{matrix}Ou melhor,\begin{matrix} P =\dfrac{43}{64} \ \ \ \tiny{\blacksquare}
\end{matrix}$• \ \text{Resolução II:}$ $\color{#3368b8}{\text{Evento Complementar}}$
Observe que a resolução acima ficou extensa e, numa prova, quase impraticável. Por isso, seguir com a ideia de probabilidade complementar é extremamente útil. Basicamente, buscamos a probabilidade de nenhum quadrado possuir cores idênticas lado a lado, o que pode ser dividido em dois casos:\begin{matrix}
\text{Caso I:}& \text{Os quadrados numa diagonal são iguais} \\
\text{Caso II:}& \text{Os quadrados numa diagonal são diferentes} \\
\end{matrix}No primeiro caso, deve-se escolher uma entre $4$ cores para pintar essa diagonal, restando $3$ cores possíveis para os demais quadrados.\begin{matrix}
\#(\text{I}) = 4 \cdot 3 \cdot 3 &\therefore& \#(\text{I}) = \text{36 eventos}
\end{matrix}Para o segundo caso, há $4$ cores para o primeiro quadrado da diagonal, assim como $3$ para o segundo. Aos demais, sabe-se que eles não podem ser iguais ao quadrados adjacentes, ou seja, os dois restantes possuem $2$ opções de cores cada.\begin{matrix}
\#(\text{I}) = 4 \cdot 3 \cdot 2 \cdot 2 &\therefore& \#(\text{I}) = \text{48 eventos}
\end{matrix}Então a probabilidade complementar é,\begin{matrix}
P^c = \dfrac{\#(\text{I}) + \#(\text{II}) }{\#W} &,& P = 1-P^c
\end{matrix}Portanto,\begin{matrix} P =\dfrac{43}{64} \ \ \ \tiny{\blacksquare}
\end{matrix}\begin{matrix}Letra \ (E)
\end{matrix}